$\psfig{figure=periodic-sphere.ps,width=10cm,bbllx=74pt,bblly=206pt,bburx=565pt,bbury=690pt,clip=}$

GdfidL v3.8: Syntax and Semantics

Warner Bruns

List of Figures

Introduction

Features:

All Computations are parallelised for MultiCore and NuMA Systems.
All Computations may be run on massively parallel Systems, such as Clusters of WhatEver.
The Device under Test may contain lossy, dispersive Materials, both for Time Domain and Eigenvalue Computations. Absorbing Boundary Conditions may be applied for lossy Eigenvalue Computations. Impedance Boundary Conditions may be applied for Time Domain Computations.
Periodic Boundary Conditions for all three cartesian Directions can be specified simultaneously for loss-free Eigenvalue Computations.
The Device under Test is approximated by generalised diagonal Fillings. The Approximation Error is reduced about by a Factor of Ten, compared to an Approximation with simple diagonal Fillings.
The Time Domain Computation and lossy Eigenvalue Computation uses "Perfectly Matched Layers" for their Absorbing Boundary Conditions.
Short Range Wakepotential Computations may be performed using a moving Window enclosing the interesting Region. The Fields are computed using a Strang-Splitting Scheme with zero Dispersion-Error for Waves travelling in strictly z-Direction, or a higher Order FDTD Scheme with low Dispersion-Error for all Kinds of Waves.
The Programs can be run interactively. The Commands are explained when you type the special Command help.
The Solver and the Postprocessor have a built-in macro Processor.
- You may define Symbols storing numerical Values or character Values.
- Arithmetic Expression Evaluator.
- You can groups of Commands as MACROs. The MACROs can have an unlimited Amount of Parameters.
- 'do-loop's are implemented.
- 'if' 'elseif' 'else' 'end if'
Almost all Commands may be abbreviated as long the Abbreviation is unique in Context.

GdfidL consists of 5 separate Programs that work together. These Programs are:

gd1 & single.gd1: These Programs read the Description of the Problem and compute resonant Fields or time dependent Fields. gd1 computes in Double Precision, while single.gd1 computes in Single Precision. single.gd1 needs somewhat less Memory and often less CPU-Time.
gd1.pp : This is the Postprocessor. It displays the Fields, computes Integrals over the Fields to compute quality Factors and the like. It also computes scattering Parameters and Wakepotentials from Data that have been computed by gd1 or single.gd1.
gd1.3dplot: This Program displays the 3D-Plots on a X11 Window and produces PostScript Files.
mymtv2: This Program displays the 1D and 2D-Plots on a X11 Window and produces PostScript Files.

mymtv2 was not written by us. It is a (slightly) modified Version of the Program plotmtv written by Kenny Toh. The original Sources for plotmtv can be found on the Internet: plotmtv can be found at ftp.x.org: /contrib/applications/Plotmtv.1.3.2.tar.Z

gd1

Typical Usage of gd1

gd1 reads its Information from the Standard Input Unit. You will normally use two or more xterms to operate gd1. In one of the xterms you edit an Inputfile that describes your Device, in the other xterm you iteratively start gd1 and try out how gd1 reacts to your Input.

gd1 reads the Description of the Device that you are interested in from stdin or from a File that you specify via include(filename). gd1 generates the Mesh and computes the resonant Fields or time dependent Fields. The Results are written to a Database that can be read by gd1.pp.

Input for gd1

gd1's Input is pure Text. You give gd1 the Information about the Problem to be analysed in distinct Sections.

The required Information that you have to give gd1 is

The Name of the Resultfile (-general).
The Borders of the computational Volume (-mesh).
The wanted Mesh-Spacing (-mesh).
The boundary Conditions at the Borders of the computational Volume
(-mesh) (-fdtd/-ports) (-eigenvalues/-ports).
The Description of the Device (-brick, -gccylinder, -ggcylinder, -gbor, -stlfile, -geofunction, -transform).
- For an Eigenvalue Computation:
  - The wanted Number of Frequencies (-eigenvalues).
  - An Estimation of the highest Frequency (-eigenvalues).
  - For lossy Eigenvalues: The location of Ports (-eigenvalues/-ports, -fdtd/-ports).
- For a Time Domain Computation:
  - The Location of Ports (-fdtd/-ports).
  - The Excitation (-fdtd/-pexcitation, -fdtd/-lcharge, -fdtd/-dipole).
  - The minimal Time to be simulated (-fdtd/-time).
  - The maximal Time to be simulated (-fdtd/-time).

The Symbols in the above Brackets indicate in which Section of gd1 you specify the required Parameters.

Behind the Scenes: When the Mesh is generated

There is no standalone Meshgenerator. When you define a geometric Primitive, the only Thing that happens immediately is that the Information about the geometric Primitive is stored in an internal Database. When you say doit in the Section -eigenvalues, in the Section -fdtd or in the Section -windowwake, the Mesh is generated on the Fly. When you display the Mesh-Filling via the Section -volumeplot, the Mesh is also generated on the Fly.

General Sections

These are the Sections where you specify Parameters that are required for every Field Computation.

In the Section -general, you specify the Name of the File where the Results shall be written to.

In the Section -mesh, you have to specify the Borderplanes of the computational Volume, and the default Mesh Spacing. You also define the boundary Conditions at the Borderplanes here.

In the Section -material, you specify the electric Properties of the Materials.

Entry Section

This is the Section you are in when you start gd1.

 ##############################################################################
 # Flags: nomenu, noprompt, nomessage,                                        #
 ##############################################################################
 # gdfidl (32) (V 3.8) (compiled Thu Sep  9 09:20:05 GMT 2021 on Host wb041a) #
 #  VshzpnIb 210909                                                           #
 ##############################################################################
 # -general        -- Output File, Annotations.                               #
 # -mesh           -- Bounding Box, Spacing, fixed Meshplanes,                #
 #                 -- Boundary Conditions.                                    #
 # -material       -- Material Properties.                                    #
 # -lgeometry      -- Load a previously used Geometry.                        #
 # ***** Geometric primitives ****                                            #
 # -brick          -- Simple rectangular Brick.                               #
 # -gccylinder     -- Circular Cylinder in general Direction.                 #
 # -ggcylinder     -- General Cylinder in general Direction.                  #
 # -gbor           -- Body of Revolution in general Direction.                #
 # -stlfile        -- CAD Import via STL-File.                                #
 # -geofunction    -- Analytic Function.                                      #
 # -transform      -- Rotations etc                                           #
 #     ( -translate, -rotate )                                                #
 # ***** Solver Sections ****                                                 #
 #  -eigenvalues   -- Resonant Fields                                         #
 #     ( -ports, -linitialfields )                                            #
 #  -fdtd          -- Time dependent Fields                                   #
 #     (-time, -ports, -pexcitation, -lcharges, -voltages, -dipole, -clouds   #
 #      -storefieldsat, -linitialfields, -fexport, -fmonitor, -smonitor       #
 #      -pmonitor, -windowwake, -decaytime )                                  #
 #  -magnetostatic -- Magnetostatic Fields (rudimentary)                      #
 #     ( -lcurrent )                                                          #
 # *******                                                                    #
 #  -volumeplot    -- Displays Mesh Filling.                                  #
 #  -cutplot       -- Displays Mesh Filling in a single Plane                 #
 # ***** Miscellanea ******                                                   #
 #  -debug         -- Specify Debug Levels                                    #
 #                                                                            #
 ##############################################################################
 # ?, end, help, __mdoit, __hwinfo                                            #
 ##############################################################################

The Menu shows all Sections. There are some Subsections, which you may also enter from within any Section, these are shown in Brackets (). You enter a Section by specifying its Name.
Example To enter the Section -general, you say:

   -general

As all Commands may be abbreviated, you may also say:

-ge

-general : Annotations, filenames

Here you specify where the Results shall be stored and where Scratchfiles shall be written to. You may also document your Project by putting descriptive Text to the Plots.

 ##############################################################################
 # Flags: nomenu, noprompt, nomessage,                                        #
 ##############################################################################
 # Section: -general                                                          #
 ##############################################################################
 # outfile    = /tmp/--username--/--SomeDirectory--/Results                   #
 # scratchbase= /tmp//gdfidl-scratch-pid=000014129-                           #
 # restartfiles= -none-                                                       #
 #   t1restartfiles=  1440         -- Minutes. When to write the first Set.   #
 #   dtrestartfiles=  1440         -- Minutes. Distance between writing.      #
 #   stopafterrestartfiles=1000000000   -- Stop after writing so often.       #
 #   singlesetofrestartfiles= no        -- yes: Write always the same Set.    #
 # text( 1)= ' '                                                              #
 # text( 2)= ' '                                                              #
 # text( 3)= ' '                                                              #
 # text( 4)= ' '                                                              #
 # text( 5)= ' '                                                              #
 # text( 6)= ' '                                                              #
 # text( 7)= ' '                                                              #
 # text( 8)= ' '                                                              #
 # text( 9)= ' '                                                              #
 # text(10)= ' '                                                              #
 # text(11)= ' '                                                              #
 # text(12)= ' '                                                              #
 # text(13)= ' '                                                              #
 # text(14)= ' '                                                              #
 # text(15)= ' '                                                              #
 # text(16)= ' '                                                              #
 # text(17)= ' '                                                              #
 # text(18)= ' '                                                              #
 # text(19)= ' '                                                              #
 # text(20)= ' '                                                              #
 # uslices= auto       -- PVM/MPI: [yes|no|auto|1length]:                     #
 #                     -- if [yes|1length] : Partition in x,y or z only.      #
 # ndpw   = auto       -- PVM/MPI: Number of Dice per Worker                  #
 # iodice = no         -- PVM    : yes: Each Worker writes its own Results.   #
 # nrofthreads= 32     -- SMP and PVM/MPI: Nr of Threads per Worker.          #
 # ngangs= 16          -- How many Teams.                                     #
 # fmeshing= no        -- [yes|no|auto]:                                      #
 #                     -- Use Files while building the Mesh.                  #
 # affinity= yes       -- SMP: yes: Enforce Core Affinity.                    #
 # spinwait= yes       -- SMP: yes: Do not release CPU when a Thread waits.   #
 # hyperthreading= yes -- SMP: no: Schedule on real Cores.                    #
 ##############################################################################
 # 2dplotopts= -geometry 690x560+10+10                                        #
 #  linecolor= 0              -- 0: foreground, 3: yellow                     #
 #  foreground= black         -- black, white                                 #
 #  background= white         -- blue, white, black                           #
 # showtext     = yes         -- (yes | no)                                   #
 # onlyplotfiles= no          -- (yes | no)                                   #
 ##############################################################################
 ## Syntax:                                                                   #
 #  weightpoint= (Ui, Wi)                                                     #
 ##############################################################################
 # ?, return, help, clearweights, weightpoint= (..)                           #
 ##############################################################################

outfile The Name of the File^1.1 where the Results shall be stored in. This File may exist. If it exists, then its GdfidL-Content will be overwritten.
scratchbase The Base Name of Scratchfiles that gd1 needs for its Operation. If you have an Environment Variable TMPDIR set, gd1 will as Default set scratchbase to the String
```
        $TMPDIR/gdfidl-scratch-pid=XXXXX-
```
Here $TMPDIR is the Value of the Environment Variable TMPDIR, and XXXXX is the numerical Value of the Process-id of gd1.
The Size of the Scratchfiles is sometimes more than the Amount of RAM that gd1 itself needs. The Scratchfiles should be located on a Disk which is directly attached to the compute Nodes. If the Scratchfiles are located on a Network attached Storage, a somewhat longer computation Time is to be expected.
If you are preparing a System for using GdfidL, have about ten Times more directly attached Scratch-Space than installed RAM on each compute Node.
restartfiles This is for preparing a long running Computation to survive a System Crash. The Value to give for restartfiles must be a valid Filename in a Filesystem, which survives a System Crash, ie. a Filesystem which is not cleared at Boot Time. If a Value for restartfiles is given, the Solver will write a Set at selected Times. There will be up to two Sets of Restartfiles. There are two Sets, because according to Murphy's Law it will happen that a System Crash occurs just while one Set is being written. In such a Case, the older Set still can be used. When the Restartfiles are written, a Comment is given about how to use the Restartfiles. Essentially this is: you have to restart the Computation on the same computer System (if using a parallel System: with the same number of Tasks, using the same Nodes, using the same Executable), with an additional Parameter on the Command Line of the Master Task. The additional Command Line Parameter is -restartfiles=NAME-OF-SET .
Writing Restartfiles and Recovering also works with PVM/MPI.
You can also use this Facility to trick out Batch Systems. You can specify that Restartfiles are to be written eg. after one Hour, and the Computation after writing the Restartfiles shall stop. You then restart such a Computation. This Way, you can have long running GdfidL Computations in a batch Queue which only accepts Jobs with less than two Hours Wall Clock Time.
- Enforcing writing of Restartfiles You may enforce Writing of Restartfiles, eg. when you have a long running Computation, and the System Administaror asks whether the System can be shut down:
  Periodically gd1 checks whether a File $HOME/gdfidl.WriteRestartFilesNowAndStop exists. If it exists, its Content is read. If the first Line contains a NonZero Number, all running Computations will write their Restartfiles and stop afterwards. If the running Computations did not have a Restartfile specified, the Content of the second Line of $HOME/gdfidl.WriteRestartFilesNowAndStop will be used as the BaseName of the Restartfiles. The Content of such a $HOME/gdfidl.WriteRestartFilesNowAndStop File:
```
    4711 # Some Nonzero Number will enforce writing of Restartfiles.
    /scratch/Forced-Restartfile
```
t1restartfiles First Time (in Minutes) to write Restartfiles.
dtrestartfiles Time Difference (in Minutes) between the Times when to write Restartfiles.
stopafterrestartfiles Number of Restartfile Sets to write. After that Number of Sets of Restartfiles has been written, the Computation will stop.
text(*)= This Annotation Text is plotted together with the Result Plots. This is especially useful for documenting eg. the Geometry Parameters of a calculation.
syntax:
text()= ANY STRING, NOT NECESSARILY QUOTED
or
text(NUMBER)= ANY STRING, NOT NECESSARILY QUOTED
- ANY STRING, NOT NECESSARILY QUOTED:
  The string to be included in the plots,
- NUMBER:
  Optional. The Line Number, where the Text should be plotted.
In the first Case, without NUMBER, the String following text()= is placed in the next free Line. In the Case with NUMBER, it is guaranteed, that the String is placed in the NUMBER.st Line. You can specify up to 20 Annotation Strings, the maximum Length of each Annotation String is 80 Characters.
ndpw= [auto|NUMBER] When computing on a Cluster,the computational Volume is subdivided in NUMBER Subvolumes per Task. If ndpw=auto, the Number of Subvolumes (dice) is chosen such that each Subvolume contains about 1 Million Grid Cells and the total Number of Subvolumes is larger than the total Number of Threads to use. The total Number of Threads to use is NROFTHREADS times the number of Nodes used for the parallel Run.
iodice= [yes|no] When computing on a Cluster,the Result of each Subvolume is stored on the local Disk of each Node. For this to work, OUTFILE must be a legal Filename on each Node. For this to be useful, OUTFILE must be on a locally attached Filesystem. This leads to faster writing of the Results, but longer Time for postprocessing of the Results.
This might be needed for very large parallel Computations where the computed electromagnetic Fields must be loaded into the Postprocessor for computing, eg. the Q-value. For very large parallel Computations, it can happen that the computed Datasets are so large, that the Postprocessor cannot handle the Amount of Data in its limited Address space (32 bit Processors). Even on 64 bit Processors, the required Memory might be larger than what is available on the used System. When iodice= yes, the Results are written to the local Disks of the compute Nodes. When the Results shall be analysed by gd1.pp, on each compute Node an instance of gd1.pp will be started to handle the local Amount of Data.
Only the PVM version of gd1.pp can be run in parallel. There is no MPI version of gd1.pp, as MPI lacks some needed Functionality.
nrofthreads= NTHREADS The Number of Threads to use. Each Thread uses one CPU-Core. The really used Number of Cores will not be larger than the Number of really available Cores on the used System.
affinity= [yes|no] If yes, gd1 attempts to schedule the Workload such that always the same Cores are used. That gives better Performance on NuMA-Systems, if the used System runs only one Instance of gd1, and essentially no other Load is present.
spinwait= [yes|no] If yes, the Threads do not release their Cores when they are waiting. This spin-wait gives better Performance if the used System runs only one Instance of gd1, and essentially no other Load is present.

Example The following specifies that the Results of the Computation shall be stored in the Database named '/Data/UserName/resultdirectory'. The Names of Scratchfiles that gd1 generates shall start with '/tmp/UserName/delete-me-'. Restartfiles shall be written every 24 hours, and the Names of the Restartfiles shall start with /Data/UserName/restartfile.
Together with the Plots that gd1.pp will produce, the Text 'Parameter is 45' and '2*Parameter is 90' shall appear.

 -general
     outfile= /Data/UserName/resultdirectory
     scratch= /tmp/UserName/delete-me-
     restartfiles= /Data/UserName/restartfile
     t1restart= 24 * 60, dtrestart= 24 * 60

 define(PARAMETER, 45)
     text(1)= Parameter is PARAMETER
     text(2)= 2*Parameter is eval(2*PARAMETER)

Example Tell GdfidL that every XX Minutes, all Data describing the current State of Computation shall be written to Files. From these Data, a Computation can be restarted. There is an Option, that after eg. two Datasets written, the Computation shall stop.^1.2 A Script, which restarts as long as GdfidL has not yet signalled that the Job is finished, is:

#!/bin/sh
#
# The Input for GdfidL shall contain a Specification
# for Restartfiles. In this Example, we do that
# via creating the './gdfidl.solver-profile', which is
# read and interpreted at the Start of Run.
 (cat > ./gdfidl.solver-profile) << UntilThisMarker
   -general
     # Write a Set of Restartfiles every 60 Minutes.
     restartfiles= /Data/UserName/restartfiles  # Where to write the Restartfiles
     t1restart= 60        # When to write the first Set of Restartfiles
     dtrestart= 60        # Wall Clock Time Difference between writing Restartfiles
     stopafterrestart= 2  # Stop after writing the second Set of Restartfiles.
UntilThisMarker
#
# The initial Run.
# Use '>' instead of '| tee Logfile' to get the Returncode of GdfidL.
# If 'tee' is used the Returncode would be the Returncode of 'tee'.
 gd1 -DWhateverYourOptions=... \
        < Inputfile > Logfile-restart
 RETURNCODE=$?
 echo RC ist $RETURNCODE
#
# While GdfidL signals that a Restart is useful, restart.
 while [ "$RETURNCODE" -eq "1" ]
 do
    gd1 -restartfiles=/Data/UserName/restartfiles.iMod-2 \
        >> Logfile-restart
    RETURNCODE=$?
 echo RC ist $RETURNCODE
    if [ "$RETURNCODE" -eq "0" ]; then
       exit 0
    fi
 done
#
 exit 0
 #######

Writing Restartfiles is useful anyway. If Restartfiles are written, one has the Chance to restart a crashed Computation which crashed because of some Failure of the Computersystem. To restart a Computation, the Restartfiles must be accessible, of course. So the Restartfiles should not be written to /tmp, or some other Filesystem which might be cleaned at System Boot Time or so.

When writing Restartfiles for the Possibility of recovering from some Failure of the System, you would not specify

    -general, stopafterrestart= 2

The writing of the Restartfiles takes some Time, Minutes or so. So the '-general, dtrestart= XX' Parameter should be significantly larger than '1'. We suggest '-general, dtrestart= 24*60'. That says: Write Restartfiles once per 24 Hours.

If such a Computation crashed, inspect the Logfile. You shall find Lines similar to:

 ###############
 # Restartfiles are to be written.
 #########################################################################
 # A Set of Restartfiles has been written.
 # To restart this Computation, start with the same Command,
 # on the same Computer System, but with the additional Parameter
 #    -restartfiles=/Data/UserName/restartfiles.iMod-1
 #########################################################################

This 'start with the same Command, on the same Computer System,' is for Safety. A Restart will work as long as the same Executables are used, the same PVM/MPI-Parameters are used, and the Restartfiles are accessible from every used Node.

-mesh : Outer Boundary Conditions, Spacings

gd1 needs to know

where the Boundaries of the computational Volume shall be,
what the default Spacing between Mesh-Planes shall be,
what the Boundary Conditions at the outer Planes of the computational Volume shall be.

You specify these Values in this Section.

 ##############################################################################
 # Flags: nomenu, noprompt, nomessage,                                        #
 ##############################################################################
 # Section -mesh                                                              #
 ##############################################################################
 ## Bounding Box:                                                             #
 #   pxlow = undefined      , pylow = undefined      , pzlow = undefined      #
 #   pxhigh= undefined      , pyhigh= undefined      , pzhigh= undefined      #
 #  volume= (undefined, undefined, undefined, undefined, undefined, undefined)#
 #      __zlowref = undefined                                                 #
 #      __zhighref= undefined                                                 #
 ## Boundary Conditions:                                                      #
 #   cxlow = electric, cylow = electric, czlow = electric                     #
 #   cxhigh= electric, cyhigh= electric, czhigh= electric                     #
 ## Periodic BC's for loss-free Eigenvalues:                                  #
 #   xperiodic= no , xphase= undefined                                        #
 #   yperiodic= no , yphase= undefined                                        #
 #   zperiodic= no , zphase= undefined                                        #
 #  fillfrom= (undefined, undefined, undefined)                               #
 # # # # #                                                                    #
 # xspacing= undefined, xminspacing= undefined                                #
 # yspacing= undefined, yminspacing= undefined                                #
 # zspacing= undefined, zminspacing= undefined                                #
 # graded  = no                                                               #
 #   xgraded= no , ygraded= no , zgraded= no                                  #
 # xqfgraded= 1.20, xdmaxgraded= undefined                                    #
 # yqfgraded= 1.20, ydmaxgraded= undefined                                    #
 # zqfgraded= 1.20, zdmaxgraded= undefined                                    #
 # perfectmesh= no                                                            #
 # geoscale= 1.0                                                              #
 ## Commands: # # # # # # # # # #                                             #
 # xfixed(N, X0, X1)  -- N fixed Meshplanes between X0 and X1                 #
 # yfixed(N, Y0, Y1)  -- N fixed Meshplanes between Y0 and Y1                 #
 # zfixed(N, Z0, Z1)  -- N fixed Meshplanes between Z0 and Z1                 #
 ##############################################################################
 # listplanes, return, help                                                   #
 ##############################################################################

pxlow, pxhigh, pylow, pyhigh, pzlow, pzhigh, volume
(Plane at XLOW ...) These Values are the Coordinates of the Planes that limit the computational Volume.
These Parameters are mandatory.
As an Alternative to specifying via pxlow etc., you can specify the Volume of your computational Volume as volume= (XL, XH, YL, YH, ZL, ZH).
gd1 ignores all Parts of Items that are specified outside of the Box with these Boundary Planes.
__zlowref, __zhighref
Special Parameters. If these Parameters are given, the Mesh is generated such that the Mesh below __zlowref and above __zhighref is translational invariant.
cxlow, cxhigh, cylow, cyhigh, czlow, czhigh
(Condition at XLOW ...) These are the Boundary Conditions at the Boundary Planes of the computational Volume. Possible Values are electric, magnetic.
xperiodic, yperiodic, zperiodic
Possible Values are yes, no. These Parameters toggle the Application of periodic Boundary Conditions between the lower and upper Boundary Planes in x-, y- or z-Direction. You can compute with more than one ?periodic= yes. This is only implemented for Eigenvalue Computations. For Time-Domain Computations, these Parameters should be set to no.
xphase, yphase, zphase
Specification of the Phase Shift (in Degrees) to enforce between the lower and upper Boundary Planes, when ?periodic= yes.
spacing
The default Spacing, that gd1 shall use for discretising the computational Volume. In between fixed Meshplanes, the Gridspacing will be about spacing.
This Parameter is mandatory.
Of Course, specifying a small Spacing will lead to a good Discretisation. Be aware however, that the Memory Requirement is proportional to and the CPU-time approximately to $1/(spacing)^{4}$ .
minspacing
The smallest Mesh-Spacing allowed.
gd1 tries to place Meshplanes approximately homogeneously within the Volume. It is guaranteed, that there are Meshplanes at the Boundary Planes of (not transformed) bricks, and where you enforce them via xfixed, yfixed, zfixed, if the Distance between such fixed Meshplanes is more than minspacing. Otherwise, one of these fixed Meshplanes is deleted. The deleted one is the Meshplane with the higher Coordinate Value.
If this Parameter minspacing is not given, gd1 uses the Value of spacing/10 instead.
graded
Possible Values are yes, no.
If graded= yes, the Space between fixed Meshplanes will be filled with a graded Mesh. The Ratio of adjacent Mesh-Spacing will be approximately the Value given for qfgraded.
The largest Mesh-Spacing will be less or equal dmaxgraded.
xgraded, ygraded, zgraded
This is the same as graded, but only that the Grid Planes with x-, y- or z-constant are considered for Grading.
qfgraded, dmaxgraded
These are the Parameters that are mentioned above in the Discussion of graded.
perfectmesh
If specified as yes, the Material Boundaries are approximated as smooth Patches. If specified as no, the Material Distribution in a Cell is approximated for each Cell as one out of 73 possible Material Distributions. The Meshing and Computation with perfectmesh= no is somewhat faster and is more thoroughly tested. In both Cases, the Error in computed Resonant Frequencies is reduced by about a Factor of Ten, as compared to the common known Approximation with diagonal Fillings. Unfortunately, in some Configurations unphysical Fields are computed when perfectmesh= yes, so use with Care. The Default is perfectmesh= no.
geoscale
Each Coordinate that you specify (each Parameter which has the dimension of a Length) is multiplied by this Factor. Each Parameter which has the Dimension of 1/Length, is multiplied by 1/geoscale.
xfixed, yfixed, zfixed
If nothing else is specified, the Meshgenerator of gd1 fills the computational Volume homogeneous (if graded= no). It is only guaranteed, that the Borders of (not transformed) bricks lie on Meshplanes. If you have a Geometry with items other than Bricks you sometimes can improve the Mesh by enforcing Meshplanes with these Commands.
Syntax:
xfixed(NUMBER, LOW, HIGH)
yfixed(NUMBER, LOW, HIGH)
zfixed(NUMBER, LOW, HIGH)
- NUMBER:
  The Number of Meshplanes to place in between LOW, HIGH. The total Number of meshplanes enforced by such a Command is exactly NUMBER. In the Case of xfixed, the Meshplanes are positioned at Positions :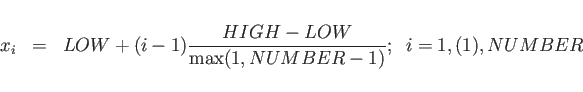
  
  $\begin{eqnarray*} x_i &=& LOW+(i-1) \frac{HIGH-LOW}{\max(1,NUMBER-1)} ;\; \; i= 1, (1), NUMBER \end{eqnarray*}$
- LOW, HIGH:
  The first and last Coordinate of the Meshplanes to be enforced.
It is possible to specify NUMBER $\le$ 0, in this Case nothing happens.
It is possible to specify NUMBER = 1, in this Case a single Meshplane at LOW is enforced.
It is not necessary that LOW is really lower than HIGH.
It is normally counterproductive to specify Regions of fixed Meshplanes. Better only specify selected Meshplanes, eg xfixed(2, X0, X1), or xfixed(1, X0, X0). Let the Solver compute on an as homogeneous Mesh as possible.
listplanes
Lists the Position of Gridplanes that will be used by gd1.

Example

 -mesh
     spacing= 1e-3
     pxlow= 1e-2, pxhigh= 0
     pylow= 2e-2, pyhigh= 0
     pzlow= 3e-2, pzhigh= 0
     
     cxlow= ele, cxhigh= mag
     cylow= ele, cyhigh= mag
     zperiodic= yes, zphase= 120

-material : electric / magnetic Properties

This Section is about specifying the Material Parameters. Materials may be perfect electric conducting (type= electric), perfect magnetic conducting (type= magnetic), electric conducting with Impedance Boundary Conditions applied (type= impedance) (type= coating), or may be loss-free or lossy Dielectrics with anisotropic Values for $\mu$ and $\varepsilon$ (type= normal). Dielectrics may have up to 10 LORENTZ-Resonances in their permittivity and permeability Functions.

 ##############################################################################
 # Flags: nomenu, noprompt, nomessage,                                        #
 ##############################################################################
 # section -material                                                          #
 ##############################################################################
 # material=  3, type= undefined                                              #
 #      ckappa= undefined        , cthickness= undefined                      #
 #                     epsr    = undefined      kappa    = undefined          #
 #                        xepsr= undefined        xkappa = undefined          #
 #                        yepsr= undefined        ykappa = undefined          #
 #                        zepsr= undefined        zkappa = undefined          #
 #                     muer    = undefined      mkappa   =       0.0          #
 #                        xmuer= undefined        xmkappa=       0.0          #
 #                        ymuer= undefined        ymkappa=       0.0          #
 #                        zmuer= undefined        zmkappa=       0.0          #
 # # Dispersion Parameters.                                                   #
 #                 feps(1)   = undefined     fmue(1)   = undefined            #
 #                   xfeps(1)= undefined       xfmue(1)= undefined            #
 #                   yfeps(1)= undefined       yfmue(1)= undefined            #
 #                   zfeps(1)= undefined       zfmue(1)= undefined            #
 #                 aeps(1)   = undefined     amue(1)   = undefined            #
 #                   xaeps(1)= undefined       xamue(1)= undefined            #
 #                   yaeps(1)= undefined       yamue(1)= undefined            #
 #                   zaeps(1)= undefined       zamue(1)= undefined            #
 #                 fegm(1)   = undefined     fmgm(1)   = undefined            #
 #                   xfegm(1)= undefined       xfmgm(1)= undefined            #
 #                   yfegm(1)= undefined       yfmgm(1)= undefined            #
 #                   zfegm(1)= undefined       zfmgm(1)= undefined            #
 ##############################################################################
 # flow  =  undefined                   -- Plot feps(f) & fmue(f) from this f #
 # fhigh =  undefined                   -- upto this f.                       #
 #  thickness=       100.0              -- .. assuming this Thickness.        #
 #   xlog= no                           -- f-Axis logarithmic.                #
 ##############################################################################
 # 2dplotopts= -geometry 690x560+10+10                                        #
 #  linecolor= 0              -- 0: foreground, 3: yellow                     #
 #  foreground= black         -- black, white                                 #
 #  background= white         -- blue, white, black                           #
 # showtext     = yes         -- (yes | no)                                   #
 # onlyplotfiles= no          -- (yes | no)                                   #
 ##############################################################################
 # return, showfeps, help                                                     #
 ##############################################################################

material
The Material Index of the Material whose Parameters are to be changed. This Number must be between 0 and 250 inclusive.
type
The Type of the Material. Possible Values are "electric", "magnetic", "impedance", "coating", "normal". An "electric" Material is treated as perfect electric conducting for the Field Computation and a "magnetic" Material is treated as perfect magnetic conducting in the Field Computation. At "impedance" or "coating" Materials, Impedance Boundary Conditions are applied when performing a Time Domain Computation.
- For Eigenvalue Computations: Materials with type= impedance are treated as perfectly conducting.
  - When the Parameter lossy= no in the Section -eigenvalues is selected, only the "epsr" and "muer" of a "normal" Material are used for the Field Computation, ie. no Losses, and no dispersive Parameters are modeled for Eigenvalue Computations. The Parameters "kappa" and "mkappa" of Materials with "type= normal" may be used by the Postprocessor, gd1.pp, to compute dielectric Losses via a perturbation Formula.
  - When the Parameter lossy= yes in the Section -eigenvalues is selected, Losses due to finite electric and magnetic Conductivities, and the dispersive Parameters of Materials with type= normal are taken into Account. Materials with type= impedance are treated as perfectly conducting.
- For Time Domain Computations, "epsr", "muer", "kappa" and "mkappa" as well as the dispersive Parameters of a "type= normal" Material are used for the Field Computation.
  At Material-Boundaries to Materials with type= impedance or type= coating Impedance-Boundary-Conditions are applied.
- Both for Time Domain and for Eigenvalue Computations, Materials with
  "type= electric" are considered perfectly conducting, and Materials with
  "type= magnetic" are considered perfectly magnetic conducting. Any specified electric Conductivities for Materials with "type= electric" or "type= impedance" are used in the Postprocessor, gd1.pp, to compute Wall Losses via a perturbation Formula.
bkappa
Only used for Materials with "type= coating". The Conductivity of the Background-Material.
cthickness
Only used for Materials with "type= coating". The Thickness of the Coating. The used Scheme assumes a Conctivity of kappa in a Thickness of cthickness, then a Conductivity of bkappa.
epsr
Only used for Materials with "type= normal". The relative Permittivity of the Material. If you specify eg. epsr= 3, all three epsr Values xepsr, yepsr and zepsr are set to the Value 3.
xepsr, yepsr, zepsr
The x-, y-, z-Value of an anisotropic Material. Only diagonal epsr Matrices can be specified.
muer
Only used for Materials with "type= normal". The relative Permeability of the Material. If you specify eg. muer= 4, all three muer Values xmuer, ymuer and zmuer are set to the Value 4.
xmuer, ymuer, zmuer
The x-, y-, z-Value of an anisotropic Material. Only diagonal muer Matrices can be specified.
kappa
The electric Conductivity of the Material in MHO/m (1/Ohm/m). If you specify eg. kappa= 5, all three kappa Values xkappa, ykappa and zkappa are set to the Value 5.
xkappa, ykappa, zkappa
The x-, y-, z-Value of an anisotropic Material. Only diagonal kappa Matrices can be specified.
mkappa
The magnetic Conductivity of the Material in Ohm/m. If you specify eg. mkappa= 6, all three kappa Values xmkappa, ymkappa and zmkappa are set to the Value 6.
xmkappa, ymkappa, zmkappa
The x-, y-, z-Value of an anisotropic Material. Only diagonal mkappa Matrices can be specified.
feps(I)
The .th LORENTZ-Frequency of a dispersive Material. If you specify eg. feps(1)= 3e9, all three feps(1) Values xfeps(1), yfeps(1) and zfeps(1) are set to the Value 3 GHz.
xfeps(I), yfeps(I), zfeps(I)
The x-, y-, z-Value of an anisotropic Material.
aeps(I)
The .th $\varepsilon$ -Amplitude of a dispersive Material.
fegm(I)
The .th $\gamma_e$ -Value of a dispersive Material.
fmue(I), amue(I), fmgm(I)
The corresponding resonant Frequency, Amplitude and $\gamma_m$ Values for a Material with LORENTZ-Resonance in the Permeability.
flow, fhigh, thickness, showfeps
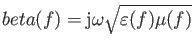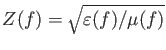
The Command showfeps creates Plots of the frequency dependend Materialparameters and of the analytical Reflection $S_{11}= \frac{Z(f) \tanh( \beta(f) L ) - Z_0 } {Z(f) \tanh( \beta(f) L ) - Z_0 }$ in the Frequency-Range between flow and fhigh, assuming a Length L=Thickness. Here: $beta(f)= {\rm j}\omega \sqrt{ \varepsilon(f) \mu(f) }$ , $Z(f) = \sqrt{ \varepsilon(f) / \mu(f) }$

Frequency dependent Materialparameters are taken into account by directly simulating the Dynamics of the Electron Hull of Molecules. For each Fieldcomponent in a dispersive Material with N Poles, the Equations of Motion (

Velocity,

Charge,

Spring-constant,

Damping Term,

Mass of the electron Hull) are solved

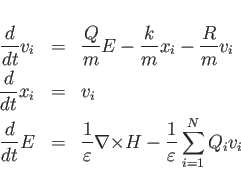
$\begin{eqnarray*} \frac{d}{dt} v_i &=& \frac{Q}{m} E - \frac{k}{m} x_i - \frac{... ...a \times }H - \frac{1}{\varepsilon } \sum\limits_{i=1}^N Q_i v_i \end{eqnarray*}$

The Parameters

Charge,

Spring-constant,

Damping Term,

Mass of the electron Hull, are computed from the User-Specified Values epsr, aeps(n), feps(n), fegm(n).

The Permittivity for an .th Order LORENTZ Medium with resonant Frequencies $\omega_n$ and damping Frequencies $\gamma_n$ reads

$\begin{displaymath} \varepsilon_r(\omega) = \varepsilon_\infty + \varepsilon_\... ...mega_n^2 } { \omega_n^2 + {\rm j}\omega \gamma_n - \omega^2 } \end{displaymath}$

(1.1)

Such a Permittivity is described with the Parameters

$$\displaystyle \verb ...$	$\textstyle :=$	$\displaystyle \varepsilon_\infty$	(1.2)
$$\displaystyle \verb ...$	$\textstyle :=$	$\displaystyle A_n$	(1.3)
$$\displaystyle \verb ...$	$\textstyle :=$	$\displaystyle \omega_n \frac{1}{ 2 \pi }$	(1.4)
$$\displaystyle \verb ...$	$\textstyle :=$	$\displaystyle \gamma_n$	(1.5)

Note: Three Materials are predefined:

Material '0' is a dielectric, whose default Values of epsr and muer are 1. This is Vacuum.
Material '1' is treated as a perfect electric Material for the Field Computations. You can change its kappa Values, but this only effects the Wall-Loss Computations of gd1.pp.
Material '2' is treated as a perfect magnetic conducting Material.

Note: While a Time Domain Computation with type= impedance Materials is performed, every 500 Timesteps the absorbed Energy in that Materials is written to GdfidL's stdout. For a Computation with four such Materials (3,5,6,8) that Output is similar to

     1.61138828e-9     1.53411444e-9  <= Time [s], IntegratedSumPowerAll [J]
     1.61138828e-9   303.51498474e-12 <= Time [s], IntegratedSumPowerMat003 [J]
     1.61138828e-9     4.27840722e-12 <= Time [s], IntegratedSumPowerMat005 [J]
     1.61138828e-9    15.01830736e-12 <= Time [s], IntegratedSumPowerMat006 [J]
     1.61138828e-9     1.21130274e-9  <= Time [s], IntegratedSumPowerMat008 [J]

The Format is such that one can grep for IntegratedSumPowerMatXXX and create without much Hassle a Datafile for further Inspection.
Example The following specifies that the Material with Number 3 shall be treated as a perfect magnetic conducting Material, the Material with Number 4 shall be a lossy Dielectric.

 -material
    material= 3
       type= magnetic
    material= 4
       type= normal, epsr= 3, kappa= 1, muer= 1

Example The following specifies that the Material with Index 10 shall be treated as a dispersive Dielectric with one LORENTZ Resonance. The frequency Dependence of the $\mu$ and the S11 of a 1/10 of a Metre thick Slab of such a Material shall be plotted.

 -material
# Dispersive Materials and Losses.
   material= 10, type= normal
  define(MUR, 1.36)
   muer= MUR, epsr= 12, kappa= 1e-6, mkappa=0
   fmue(1)= 0.61e9, amue(1)= 460/MUR/MUR, fmgm(1)= 116e9
       flow= 0.1e9, fhigh= 10e9, thickness= 0.1, xlog= yes,
       showfeps # Show the resulting fEps & fMue

To compute the Time Domain Field with dispersive Materials:

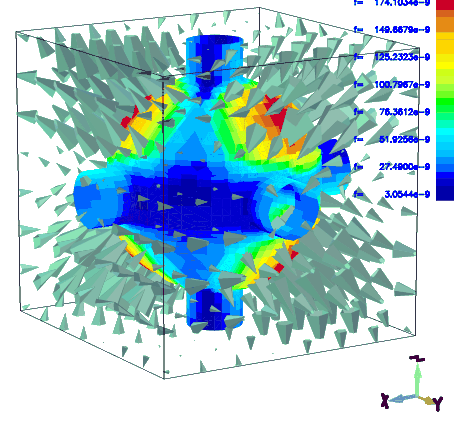
 gd1 < /usr/local/gd1/examples-from-the-manual/dispersiveMue-TEM.gdf | tee logfile

We get three Plots. Figure 1.1 shows the real Part, figure 1.2 shows the imaginary Part of the frequency dependent Muer(f). Figure 1.3 shows the Reflection that a Slab of finite Thickness L=0.1 Metres of such a Material gives for a perpendicular incident TEM-wave. The numerically computed Reflection of a such a Slab is given in Figure 1.4.

**Figure 1.1:** The real Part of the frequency dependent Muer(f).
$\begin{figure}\epsfig{figure=dispersivMue-Re.ps,width=15cm,bbllx=0pt,bblly=43pt,bburx=776pt,bbury=575pt,clip=}\end{figure}$

**Figure 1.2:** The imaginary Part of the frequency dependent Muer(f).
$\begin{figure}\epsfig{figure=dispersivMue-Im.ps,width=15cm,bbllx=0pt,bblly=43pt,bburx=776pt,bbury=575pt,clip=}\end{figure}$

**Figure 1.3:** The analytical Reflection from a finite Slab of dispersive Material.
$\begin{figure}\epsfig{figure=dispersivMue-S11-analytisch.ps,width=15cm,bbllx=0pt,bblly=43pt,bburx=776pt,bbury=575pt,clip=}\end{figure}$

**Figure 1.4:** The numerical Reflection from a Slab of finite Thickness.
$\begin{figure}\epsfig{figure=dispersivMue-S11-numerisch.ps,width=15cm,bbllx=0pt,bblly=43pt,bburx=776pt,bbury=575pt,clip=}\end{figure}$

Example The following specifies that the Material with Index 3 shall be treated as a dispersive Dielectric with four LORENTZ Resonances. The frequency Dependence of the epsr and the S11 of a 0.1 Metres thick Slab of such a Material shall be plotted.

 -material
# Dispersive Materials and Losses.
# To have Re(epsr) about 10 and Im(epsr) about 1 in 10-40GHz:
 define(EPSQ, 10**2)
     material= 3, type= normal, epsr= 10, muer= 1, kappa= 1
 kappa= 0
 define(i, 0)
 define(i, i+1) feps(i)= 10e9, aeps(i)= 1.1/EPSQ, fegm(i)= 100e9
 define(i, i+1) feps(i)= 20e9, aeps(i)= 0.42/EPSQ, fegm(i)= 100e9
 define(i, i+1) feps(i)= 30e9, aeps(i)= 0.26/EPSQ, fegm(i)= 100e9
 define(i, i+1) feps(i)= 40e9, aeps(i)= 0.28/EPSQ, fegm(i)= 100e9

     flow= 1e9, fhigh= 70e9, showfeps

To compute the Time Domain Field with dispersive Materials:

 gd1 < /usr/local/gd1/examples-from-the-manual/dispersiveEps-TEM.gdf | tee logfile

We get three Plots. Figure 1.5 shows the real Part, figure 1.6 shows the imaginary Part of the frequency dependent epsr(f). Figure 1.7 shows the Reflection that a 0.1 Metres thick Slab of such a Material would produce for a perpendicular incident TEM-wave. The numerically computed Reflection of a thick Slab of such a Material is given in Figure 1.8.

**Figure 1.5:** The real Part of the frequency dependent epsr.
$\begin{figure}\epsfig{figure=dispersiv-Re.ps,width=15cm,bbllx=0pt,bblly=43pt,bburx=776pt,bbury=575pt,clip=}\end{figure}$

**Figure 1.6:** The imaginary Part of the frequency dependent epsr.
$\begin{figure}\epsfig{figure=dispersiv-Im.ps,width=15cm,bbllx=0pt,bblly=43pt,bburx=776pt,bbury=575pt,clip=}\end{figure}$

**Figure 1.7:** The analytical Reflection from a finite Slab of dispersive Material.
$\begin{figure}\epsfig{figure=dispersiv-S11-analytisch.ps,width=15cm,bbllx=0pt,bblly=43pt,bburx=776pt,bbury=575pt,clip=}\end{figure}$

**Figure 1.8:** The numerical Reflection from a Slab of finite Thickness.
$\begin{figure}\epsfig{figure=dispersiv-S11-numerisch.ps,width=15cm,bbllx=0pt,bblly=43pt,bburx=776pt,bbury=575pt,clip=}\end{figure}$

Example The following specifies that the Material with Index 10 shall be treated as a dispersive Dielectric with two LORENTZ Resonances. The frequency Dependence of the muer and the S11 of a 20 mm Slab of such a Material shall be plotted.

 -material
# Dispersive Materials and Losses.
   material= 10, type= normal
  define(MUR, 1.36)
   muer= MUR, epsr= 1, kappa= 0, mkappa=0

   fmue(1)= 1e9, amue(1)= 200/MUR/MUR, fmgm(1)= 800.0e9
   fmue(2)= 2e9, amue(2)= 30/MUR/MUR, fmgm(2)= 80.0e9
    flow= 1e6, fhigh= 1400e6, xlog= yes, showfeps # Show the resulting fEps, fMue

To compute the Time Domain Field with dispersive Materials:

 gd1 < /usr/local/gd1/examples-from-the-manual/dispersiveMue2-TEM.gdf | tee logfile

We get three Plots. Figure 1.9 shows the real Part, figure 1.10 shows the imaginary Part of the frequency dependent Muer(f). Figure 1.11 shows the Reflection that a Slab of such a Material would produce for a perpendicular incident TEM-wave. The numerically computed Reflection of a 20 mm Slab of such a Material is given in Figure 1.12.

**Figure 1.9:** The real Part of the frequency dependent Muer.
$\begin{figure}\epsfig{figure=Oscar-Frasciello-Re.ps,width=15cm,bbllx=0pt,bblly=43pt,bburx=776pt,bbury=575pt,clip=}\end{figure}$

**Figure 1.10:** The imaginary Part of the frequency dependent Muer.
$\begin{figure}\epsfig{figure=Oscar-Frasciello-Im.ps,width=15cm,bbllx=0pt,bblly=43pt,bburx=776pt,bbury=575pt,clip=}\end{figure}$

**Figure 1.11:** The analytical Reflection from a Slab of dispersive Material.
$\begin{figure}\epsfig{figure=Oscar-Frasciello-S11-analytisch.ps,width=15cm,bbllx=0pt,bblly=43pt,bburx=776pt,bbury=575pt,clip=}\end{figure}$

**Figure 1.12:** The numerical Reflection from a Slab of dispersive Material.
$\begin{figure}\epsfig{figure=Oscar-Frasciello-S11-numerisch.ps,width=15cm,bbllx=0pt,bblly=43pt,bburx=776pt,bbury=575pt,clip=}\end{figure}$

-lgeometry : Load a previously used Geometry

This Section enables the Loading of the Grid and Material Filling of a previous Computation to be used for the current Computation.

 ##############################################################################
 # Flags: nomenu, noprompt, nomessage,                                        #
 ##############################################################################
 # Section: -lgeometry                                                        #
 ##############################################################################
 # infile = -none-                                                            #
 # xmirror= none              -- [none,low,high]                              #
 # ymirror= none              -- [none,low,high]                              #
 #                                                                            #
 #                                                                            #
 ##############################################################################
 # ?, doit, return, end, help                                                 #
 ##############################################################################

infile= NAME_OF_A_RESULTFILE:
The Name of the outfile of a previous Computation.
xmirror= [none, low, high]:
If xmirror= low , the Grid and the geometric Items are mirrored on the lower x-Plane. If xmirror= high , the Grid and the geometric Items are mirrored on the higher x-Plane. This allows the loading of a magnetostatic or resonant Field computed with using Planes of Symmetry to be loaded for a Particle in Cell Computation where, for most Cases, no Planes of Symmetry can be used.
ymirror= [none, low, high]:
doit:
- The Shapes,
- the Coordinates of the Meshplanes,
- the Materialparameters,
- the Coordinates of the Borders of the computational Volume
- and the Boundary Conditions
are read from the 'infile'.

Note: If you load a Geometry via -lgeometry, all previous defined Geometric items are lost. You should only redefine Material Parameters after loading a Grid via -lgeometry.

Geometric Primitives

-brick: A rectangular Brick

A Brick is a rectangular Box, with its Edges parallel to the cartesian Coordinate Axes. If you need to model a Brick with Edges in other Directions, you can use the -rotate Section to rotate the Brick in any Direction.

 ##############################################################################
 # Flags: nomenu, noprompt, nomessage,                                        #
 ##############################################################################
 # section -brick                                                             #
 ##############################################################################
 # material=  1, sloppy= no                                                   #
 # whichcells= all, taboo= none                                               #
 #     show= off    -- [off|now|later|all]                                    #
 #     name= brick-000000000                                                  #
 # xlow = undefined     , ylow = undefined     , zlow = undefined             #
 # xhigh= undefined     , yhigh= undefined     , zhigh= undefined             #
 # # # # #                                                                    #
 # volume= (undefined, undefined, undefined, undefined, undefined, undefined) #
 ##############################################################################
 # doit, return, help                                                         #
 ##############################################################################

material
The Material Index that shall be assigned to the Volume that makes up the Brick.
sloppy
Possible Values are yes, no. If no, Meshplanes are enforced at the Borderplanes of the Brick. For a Brick which is rotated, sloppy=no might give unexpected Results.
whichcells
Possible Values are all, or a Material-Index. If whichcells= all, all Volume inside the Brick is assigned the Material-Index, provided the former Material is not taboo. If whichcells is a Material-Index, only the Parts of the Brick that are currently filled with the given Index are assigned the new Material-Index.
taboo
Possible Values are none, or a Material-Index. If taboo= all, all Volume inside the brick is assigned the Material-Index. If taboo is a Material-Index, only the parts of the brick that are currently filled with another Index than the given Index are assigned the new Material-Index.
show
Flag, specifying whether an Outline of the specified Brick shall be displayed.
If show=off, no Outline will be displayed.
If show=later, the Outline of the Brick will be shown later, together with Outlines of other specified Items. If show=all is present, the Outlines of all other specified Items bricks gccylinders, ggcylinders and gbors found in the Inputstream so far where show was not off will be displayed.
xlow, xhigh, ylow, yhigh, zlow, zhigh, volume
The Coordinates of the bounding Planes of the Brick. As an Alternative to specifying via xlow.., you can specify the Volume of the brick as
volume= (XL, XH, YL, YH, ZL, ZH).
doit
Puts the current Data into the Meshing Database.

Example

 # /usr/local/gd1/examples-from-the-manual/brick-example.gdf
 -general
     outfile= /tmp/UserName/example
     scratch= /tmp/UserName/scratch

 -mesh
     pxlow= -1e-2, pxhigh= 3e-2
     pylow= -1e-2, pyhigh= 2e-2
     pzlow= -0.1e-2, pzhigh= 2e-2
     
     cxlow= ele, cxhigh= mag
     cylow= ele, cyhigh= mag
     czlow= ele, czhigh= mag

     spacing= 1e-3

 -brick
     material= 1, sloppy= no
        xlow= 0, xhigh= 1.1e-2
        ylow= 0, yhigh= 1.5e-2
        zlow= 0, zhigh= 0.8e-2
     doit

 -transform,
      -translate, offset= ( 1.5e-2, 0, 0 ), doit
      -rotate, axis= ( 1, 0, 0 ), angle= -45, doit
 -brick, material= 3, sloppy= yes, doit

 -volumeplot
     scale= 3
     doit

**Figure 1.13:** A simple Brick, and the same Brick-Data translated and rotated.
$\begin{figure}\begin{center}\quad \quad \psfig{figure=brick-example.ps,width=18cm,bbllx=-2pt,bblly=-2pt,bburx=716pt,bbury=556pt,clip=} \end{center} \end{figure}$

-gccylinder: A circular Cylinder in general Direction

A gccylinder is a circular Cylinder, with its Axis in some arbitrary Direction.

 ##############################################################################
 # Flags: nomenu, noprompt, nomessage,                                        #
 ##############################################################################
 # section -gccylinder                                                        #
 ##############################################################################
 # material  =  1                                                             #
 # whichcells= all, taboo= none                                               #
 #     show= off    -- [off|now|later|all]                                    #
 #     name= gccyl-000000000                                                  #
 # radius    = undefined                                                      #
 # length    = undefined                                                      #
 # origin    = ( undefined, undefined, undefined )                            #
 # direction = ( undefined, undefined, undefined )                            #
 ##############################################################################
 # doit, return, help                                                         #
 ##############################################################################

material
The Material Index, that shall be assigned to the Volume, which makes up the gccylinder.
whichcells
Possible Values are all, or a Material-Index. If whichcells=all, all Volume inside the cylinder is assigned the Material-Index, provided the former Material is not taboo. If whichcells is a Material-Index, only the Parts of the Cylinder that are currently filled with the given Index are assigned the new Material-Index.
taboo
Possible Values are none, or a Material-Index. If taboo=none, all Volume inside the Cylinder is assigned the Material-Index. If taboo is a Material-Index, only the Parts of the cylinder that are currently filled with another Index than the given taboo-Index are assigned the new Material-Index.
show
Flag, specifying whether an Outline of the specified gccylinder shall be displayed.
If show=off, no Outline will be displayed.
If show=later, the Outline of the gccylinder will be shown later, together with Outlines of other specified Items. If show=all is present, the Outlines of all other specified Items bricks gccylinders, ggcylinders and gbors found in the Inputstream so far where show was not off will be displayed.
radius
The Radius of the circular Cylinder.
length
The Length of the Cylinder.
origin
The Coordinates of the Center of the Foot-Circle of the circular Cylinder.
direction
The Direction of the Cylinder's Axis.
doit
Puts the current Data as the data of a circular Cylinder into the Meshing Database.

Note: You can revert the Direction of the Cylinder by negating the direction, or (easier) by negating the length.
Note: If you want eg. a Quarter of a circular Cylinder, you have to use -gbor, see Pages

ff.
Example

 # /usr/local/gd1/examples-from-the-manual/gccylinder-example.gdf

 -general
     outfile= /tmp/UserName/example
     scratch= /tmp/UserName/scratch-

 -mesh
     pxlow= 0, pxhigh= 1e-2
     pylow= 0, pyhigh= 2e-2
     pzlow= 0, pzhigh= 1.5e-2
     
     cxlow= ele, cxhigh= mag
     cylow= ele, cyhigh= mag
     czlow= ele, czhigh= mag

     spacing= 0.2e-3

 -gccylinder
     material= 5, radius= 3e-3, length= 7e-3
     origin= ( 0.5e-2, 0.3e-2, 0.6e-2 )
     direction= ( -0.4, 1.5, 0.4 )
     doit
        
 -volumeplot
     scale= 3
     doit

**Figure 1.14:** A simple gccylinder, with its Axis directing towards (-0.4, 1.5, 0.4).
$\begin{figure}\centerline{ \psfig{figure=gccylinder-example.ps,width=18cm,bbllx=-2pt,bblly=-2pt,bburx=716pt,bbury=556pt,clip=} }\end{figure}$

Example

 # /usr/local/gd1/examples-from-the-manual/gccylinder-example2.gdf

 define(VeryLarge, 10000)

 -general
    outfile= /tmp/UserName/example
    scratch= /tmp/UserName/scratch

    text()= A Chain of circular Cylinders
    text()= The Cylinders are partly outside of the bounding Box.

 -mesh
    pxlow= -0.8, pxhigh= 10
    pylow= -2, pyhigh= 2
    pzlow= -0, pzhigh= 1.8

    spacing= 8e-2

 -brick
    material= 0
    volume= ( -VeryLarge, VeryLarge, \
              -VeryLarge, VeryLarge, \
              -VeryLarge, VeryLarge )
    doit

 define(RADIUS, 0.6)
 -gccylinder
    length= 1.7
    radius= RADIUS
    do jj= 0, 9, 1
       material= jj+3
       origin= ( jj*1.5*RADIUS, 0, 0 )
 define(PHI, jj*22.5*@pi/180 )
       direction= ( 0, cos(PHI), sin(PHI) )
       doit
    end do

 -volumeplot
    eyeposition= ( 1.0, 2.30, 2 )
    scale= 5
    doit

**Figure 1.15:** A Chain of simple circular Cylinders. Each Cylinder has its Axis pointing in a different Direction.
$\begin{figure}\centerline{ \psfig{figure=gccylinder-example2.ps,width=18cm,bbllx=-2pt,bblly=-2pt,bburx=716pt,bbury=556pt,clip=} }\end{figure}$

-ggcylinder: A general Cylinder in general Direction

A ggcylinder is a general Cylinder with a Footprint (Cross-Section) described as a general Polygon. This Footprint is swept along an Axis in a general Direction, additionally, this Footprint can shrink or expand along this Axis, additionally, this Footprint can be rotated along the Axis, additionally, only Parts of the ggcylinder that fulfill some additional Condition will be filled.

 ##############################################################################
 # Flags: nomenu, noprompt, nomessage,                                        #
 ##############################################################################
 # section -ggcylinder                                                        #
 ##############################################################################
 # material   =  1                                                            #
 # whichcells = all, taboo= none                                              #
 #     show   = off                     -- (off | all | later | now)          #
 #     name   = ggcyl-000000000                                               #
 #   fixpoints= no                      -- (yes|no)                           #
 #     inside = yes                     -- (yes|no)                           #
 # originprime    = ( 0.0, 0.0, 0.0 )                                         #
 # xprimedirection= ( 1.0, 0.0, 0.0 )                                         #
 # yprimedirection= ( 0.0, 1.0, 0.0 )                                         #
 #   zprimedirection= ( 0.0, 0.0, 1.0 )                                       #
 #   usezprimedirection= no             -- (yes|no)                           #
 # range      = ( undefined, undefined )                                      #
 # pitch      = 0.0                     -- [Degs/m]                           #
 # xexpgrowth = 0.0                                                           #
 # yexpgrowth = 0.0                                                           #
 # xslope     = 0.0                     -- (x2/x1-1)/len [1/m]                #
 # yslope     = 0.0                     -- (y2/y1-1)/len [1/m]                #
 # xscaleprime= 1.0                                                           #
 # yscaleprime= 1.0                                                           #
 # zxscaletablefile= -none-
 # zyscaletablefile= -none-
 #    deltaphi= 4.0                     -- Arc and Ellipse Resolution [Degs]  #
 ##############################################################################
 ## Syntax:                                                                   #
 #  point= (Xi, Yi)                                                           #
 #  arc, radius= RADIUS, type= [clockwise | counterclockwise]                 #
 #       size= [small | large ]                                               #
 #       deltaphi= 5                                                          #
 #  ellipse, center= (X0, Y0), size= [small | large ]                         #
 #       deltaphi= 5                                                          #
 ##############################################################################
 # doit, return, help, list, reset, clear                                     #
 ##############################################################################

material=MAT:
The Material Index that shall be assigned to the Volume.
whichcells
Possible Values are all, or a Material-Index.
If whichcells=all, all Volume inside the ggcylinder is assigned the Material-Index, provided the former Material is not taboo. If whichcells is a Material-Index, only the Parts of the ggcylinder that are currently filled with the given Index are assigned the new Material-Index.
taboo
Possible Values are none, or a Material-Index.
If taboo=none, all Volume inside the ggcylinder is assigned the Material-Index. If taboo is a Material-Index, only the Parts of the ggcylinder that are currently filled with another Index than the given Index are assigned the new Material-Index.
originprime:
The Coordinates of the Origin of the ggcylinder.
xprimedirection:
The Direction of the x'-Axis of the Polygon that describes the Footprint.
yprimedirection:
The Direction of the y'-Axis of the Polygon that describes the Footprint. The y'-Direction will internally be enforced to be perpendicular to the x'-Direction.
usezprimedirection= [yes|no]:
If usezprimedirection= yes, the Axis of the Cylinder is not computed from the Cross Product of xprimedirection and yprimedirection, but is taken to be the Direction given by zprimedirection= ( XZ, YZ, ZZ ).
zprimedirection= ( XZ, YZ, ZZ ):
If usezprimedirection= yes, the Axis of the Cylinder has the Direction given by
zprimedirection= ( XZ, YZ, ZZ ). If usezprimedirection= no, the given Values are not used and the Direction is given by the Cross Product of
xprimedirection and yprimedirection.
range:
Start and End Values of the z'-Coordinate of the Cylinder in the Coordinate System of xprimedirection,yprimedirection,(xprime $\times$ yprime), relative to originprime.
pitch:
Phase Shift in Degrees/m. The Footprint will be rotated along the Axis.
xexpgrowth, yexpgrowth
Alpha of the exponential Growth of the x-Coordinates, resp. y-Coordinates of the Footprint along the Axis in 1/m.
xslope, yslope:
Factor of the linear Growth of the x'-Coordinates, resp. y'-Coordinates of the Footprint along the Axis in 1/m.
xscaleprime, yscaleprime:
The x'-Coordinates, resp. y'-Coordinates of the Footprint are multiplied by these Factors.
zxscaletablefile, zyscaletablefile:
The x'-Coordinates, resp. y'-Coordinates of the Footprint are multiplied by these Factors. The Factors are given as Tables in external Files. The Format is: first Column z-Coordinate, second Column the Scaling.
inside:
Flag, specifying whether the Inside of the ggcylinder shall be assigned Material Index MAT, or whether the Volume outside of it shall be changed.
show:
Flag, specifying whether an Outline of the specified ggcylinder shall be displayed.
If show=off, no Outline will be displayed.
If show=later, the Outline of the ggcylinder will be shown later, together with Outlines of other specified Items. If show=all is present, the Outlines of all other specified Items bricks gccylinders, ggcylinders and gbors found in the Inputstream so far where show was not off will be displayed.
fixpoints
Ensure Meshplanes at the Points of the Footprint, both at the Beginning and the End of the Extrusion Range. This is seldom useful.
point= (XI, YI):
XI, YI are the Coordinates of the i.th Point in the Polygon that describes the Footprint of the ggcylinder. There have to be minimum 3 Points, or 2 Points and an Arc or 2 Points and an Ellipse.
arc:
(optional):
Indication, that there shall be a circular Arc from the Point that was specified before, to the Point that will be specified as the next Point.
In Order to determine the Arc between two Points, three Parameters are necessary: The Radius of the Arc, whether the Connection is Clockwise or Counterclockwise, and whether the Connection shall take the large Path or the small Path.
- radius= RADIUS:
  The Points are to be connected by an Arc with Radius=RADIUS
- size= [small | large] (optional):
  Indication, whether the Connection between the two Points shall be on the smaller or the larger Side of the Arc.
- type= [clockwise | counterclockwise]:
  Indication, whether the Connection between the two Points shall proceed Clockwise or Counterclockwise along the Arc.
- deltaphi:
  The wanted Resolution of the Arc or Ellipse in Degrees. A circular Arc or a Part of an Ellipse is internally discretised as a Polygon. The deltaphi Parameter controls the Resolution of that Discretisation.
clear:
Clears the current Polygon Path.
doit:
Puts the current Data as the Data of a general Cylinder into the meshing Database.

Example The following decribes a Cavity with rounded Corners.

 # /usr/local/gd1/examples-from-the-manual/ggcylinder-example.gdf

 -general
    outfile= /tmp/UserName/example
    scratch= /tmp/UserName/scratch

    text()= We use 'fixpoints= yes'
    text()= to ensure Meshplanes at the Points of the Polygon.
    text()=
    text()= We use a graded Mesh.

 -mesh
    spacing= 100e-6
    graded= yes, dmaxgraded= 263.3e-6
    pxlow= -5e-3, pxhigh= 5e-3
    pylow= -4.34e-3, pyhigh= 0
    pzlow= -1.6665e-3, pzhigh= 1.6665e-3

    cxlow= ele, cxhigh= mag
    cylow= ele, cyhigh= mag
    czlow= ele, czhigh= ele

 -ggcylinder

    material= 7
    originprime= ( 0, 0, 0 )
    xprimedirection= ( 1, 0, 0 )
    yprimedirection= ( 0, 0, 1 )
    range= ( -4.2e-3, 4.2e-3 )

    clear  # Clear the Polygon-List, if any
    point= ( -3.3405e-3, -816.5e-6 )
       arc, radius= 500.0e-6, type= counterclockwise, size= small
    point= ( -2.8405e-3, -1.3165e-3 )
    point= (  2.8405e-3, -1.3165e-3 )
       arc
    point= (  3.3405e-3, -816.5e-6 )
    point= (  3.3405e-3,  816.5e-6 )
       arc
    point= (  2.8405e-3, 1.3165e-3 )
    point= ( -2.8405e-3, 1.3165e-3 )
       arc
    point= ( -3.3405e-3,  816.5e-6 )

    fixpoints= yes # Ensure Mesh-Planes at the Points of the Polygon.
    doit

 -volumeplot
    scale= 4
    doit

**Figure 1.16:** A simple ggcylinder
$\begin{figure}\centerline{ \psfig{figure=ggcylinder-example.ps,width=18cm,bbllx=-2pt,bblly=-2pt,bburx=716pt,bbury=556pt,clip=} } \end{figure}$

Example The following decribes a twisted rectangular Waveguide.

 # /usr/local/gd1/examples-from-the-manual/ggcylinder-twisted.gdf

 define(LargeNumber, 10000)

 define(LENGTH, 10e-3)
 define(WGW, 2.54e-3 )
 define(WGH, WGW/2 )

 -general
    outfile= /tmp/UserName/example
    scratch= /tmp/UserName/scratch

    text()= A Waveguide-Twist
    text()= Waveguide-Width : WGW
    text()= Waveguide-Height: WGH

 -mesh
    spacing= WGW/80
    pxlow= -1e-3, pxhigh= LENGTH+1e-3
    pylow= -WGW*0.6, pyhigh= 0.6*WGW
    pzlow= -WGW*0.6, pzhigh= 0.6*WGW


 define(EL, 10)
 -material, material= EL, type= electric 
 -brick
    #
    # Fill the Universe with Metal:
    #
    material= EL
       volume= ( -LargeNumber, LargeNumber, \
                 -LargeNumber, LargeNumber, \
                 -LargeNumber, LargeNumber )
    doit

 -ggcylinder
    #
    # The twisted Waveguide.
    # We use a rectangular Footprint,
    # and specify a Pitch.
    # The Footprint shall rotate by -90 Degrees, over a length of LENGTH.
    #


    material= 0
    originprime= ( 0, 0, 0 )
    xprimedirection= ( 0, 1, 0 )
    yprimedirection= ( 0, 0, 1 )
    range= ( 0, LENGTH )
    pitch= -90/LENGTH

    clear  # Clear the previous Polygon-List, if any.
    point= ( -WGW/2, -WGH/2 )
    point= (  WGW/2, -WGH/2 )
    point= (  WGW/2,  WGH/2 )
    point= ( -WGW/2,  WGH/2 )
    doit

 -volumeplot
    eyeposition= ( 1, 2, 1.3 )
    scale= 4.5
    doit

**Figure 1.17:** A simple ggcylinder, with a Pitch.
$\begin{figure}\centerline{ \psfig{figure=ggcylinder-twisted.ps,width=18cm,bbllx=-2pt,bblly=-2pt,bburx=716pt,bbury=556pt,clip=} } \end{figure}$

Example The following decribes a Transition from a circular Waveguide to an elliptical Waveguide.

 # /usr/local/gd1/examples-from-the-manual/ggcylinder-circular-to-elliptic.gdf

 define(LargeNumber, 10000)

 define(LENGTH, 10e-3)
 define(RADIUS1, 2.54e-3 ) define(RADIUS2, 5.0e-3  )
 -general
    outfile= /tmp/UserName/example
    scratch= /tmp/UserName/scratch

    text()= A Transition from a circular Waveguide to an elliptical One.
    text()= The Bounding box is specified such,
    text()= that only the Part below the Plane z=0 is discretised.

 -mesh
    spacing= RADIUS1/20
    pxlow= -1e-3, pxhigh= LENGTH+1e-3
    pylow= -RADIUS2*1.0, pyhigh= RADIUS2*1.0
    pzlow= -RADIUS1*1.1, pzhigh= 0


 define(EL, 10)
 -material, material= EL, type= electric 
 -brick
    #
    # Fill the Universe with Metal:
    #
    material= EL
       volume= ( -LargeNumber, LargeNumber, \
                 -LargeNumber, LargeNumber, \
                 -LargeNumber, LargeNumber )
    doit

 -ggcylinder
    #
    # The Waveguide.
    # We use a circular Footprint,
    # and specify a Slope, different in x- and y
    #
    material= 0
    originprime= ( 0, 0, 0 )
    xprimedirection= ( 0, 1, 0 )
    yprimedirection= ( 0, 0, 1 )
    range= ( 0, LENGTH )
# xlingro 1+(RADIUS2/RADIUS1-1)/LENGTH
    xslope= (RADIUS2/RADIUS1-1)/LENGTH
    yslope= 0

    clear  # Clear the previous Polygon-List, if any.
    point= ( -RADIUS1, 0 )
      arc, radius= RADIUS1, size= large, type= counterclockwise
    point= (  RADIUS1, 0 )
      arc
    point= ( -RADIUS1, 0 )
    doit

 -volumeplot
    eyeposition= ( 2, 1, 1.8 )
    scale= 3
    doit

**Figure 1.18:** A simple ggcylinder, with different Growthfactors for x and y.
$\begin{figure}\centerline{ \psfig{figure=ggcylinder-circular-to-elliptic.ps,width=18cm,bbllx=-2pt,bblly=-2pt,bburx=716pt,bbury=556pt,clip=} } \end{figure}$

Example The following decribes a elliptical Wedge where the Axis of the ggcylinder is in the z-Direction, while the Plane Normal of the Wedge is tilted.

 # /usr/local/gd1/examples-from-the-manual/ggcylinder-usezprimedirection.gdf

 define(INF, 1000)
 define(STPSZE, 0.5e-3)       # Define the Mesh Step Size, 0.5 mm
 
 #
 # Description of the Flange Geometry.
 #
 define(FlangeGap, 10e-3 )      # Gap of the Flange Joint.
 define(FlangeD0, 80e-3)        # Diameter of Gasket Seal.
 define(Width, FlangeGap/2 )    # 1/2 Width of Flange Gap in z-Axis.
 define(FlangeRadius, FlangeD0/2 )
 define(AxisA  , 70e-3/2 )      # 1/2 *major Diameter of interior Ellipse.
 define(AxisB  , 32e-3/2 )      # 1/2 *minor Diameter of interior Ellipse.

  #--- Parameters related to a tilted Flange Joint ---
 define(ZW, 10e-3)                      # z-Deviation from the y-Axis.
 define(Theta, atan(ZW/FlangeRadius) )  # Angle between y-Axis and y'-Axis.
 define(RR, FlangeRadius/cos(Theta) )   # Radius of the tilted Cylinder.
 define(LL, Width/cos(Theta) )          # Half Length of tilted Cylinder.


 ###
 ### We enter the Section "-general"
 ### Here we define the Name of the Database where the
 ### Results of the Computation shall be written to.
 ###    (outfile= )
 ### We also define what Names shall be used for Scratchfiles.
 ###    (scratchbase= )
 ###
 -general
    outfile= /tmp/UserName/bla
    scratch= /tmp/UserName/scratch-

    text()= Flange Gap= FlangeGap
    text()= Mesh= STPSZE m
    text()= tilt Angle of Flange= eval(Theta*180/@pi) [Degrees]

 ###
 ### We define the default Mesh-Spacing,
 ### we define the Borders of the computational Volume.
 ###
 define(Zmin, -4e-2)
 define(Zmax,  4e-2)
 -mesh
   spacing= STPSZE
   pxlow= -5e-2, pxhigh= 0
   pylow= -4e-2, pyhigh= 4e-2
   pzlow= Zmin, pzhigh= Zmax

 #####
 # Specify that the Material Index '3' describes a perfect conducting Material.
 -material, material= 3, type= electric

 ## 
 ## Fill the Universe with Metal.
 ##
 -brick, material= 3, volume= ( -INF,INF, -INF,INF, -INF,INF ), doit

 ##
 ## Step 1: Carve out a tilted circular Box.
 ##
  -ggcylinder         # A Parallelogram Gap with a tilt Angle.
     material= 0
     origin= ( 0, 0, 0 )
     xprimedirection= ( 1, 0, 0 )
     yprimedirection= (0, cos(Theta), sin(Theta) )
 zprimedirection= ( 0, 0, 1 ), usezprimedirection= yes
     range= ( -LL, LL )

     clear
     point= ( -RR, 0 )
       arc, radius= RR,type= counterclockwise, size= small
     point= (  RR, 0 )
       arc, radius= RR,type= counterclockwise, size= smal 
     point= ( -RR, 0 )
     show= later
     doit
 usezprimedirection= no # Switch back to the Default, 'no'.

##
## Step 2: Creating the interior Footprint of elliptic Beampipe(hollow)
##
-ggcylinder
   material= 0
   origin= ( 0, 0, 0 )
   xprimedirection= ( 1, 0, 0 )
   yprimedirection= ( 0, 1, 0 )
   range= (Zmin-2*STPSZE, Zmax+STPSZE)
   xslope= 0, yslope= 0

   clear  # Clear any old Polygon-Description of the Footprint.
    # point= (x', y')
   point= ( 0, -AxisB),
     ellipse, center= ( 0, 0 ),
   point= ( AxisA, 0 ),
     ellipse,
   point= ( 0, AxisB ),
     ellipse,
   point= ( -AxisA, 0 ),
     ellipse,
   point= ( 0, -AxisB ),
# show= all
   doit

 ############

 -volumeplot
    eyeposition= ( 1, -0.5, 0.5 )
    scale= 3
    doit

**Figure 1.19:** A simple ggcylinder, with zprimedirection different from the Footprints Plane Normal.
$\begin{figure}\centerline{ \psfig{figure=ggcylinder-usezprimedirection.ps,width=18cm,bbllx=-2pt,bblly=-2pt,bburx=716pt,bbury=556pt,clip=} } \end{figure}$

Example The following decribes a Cosine-Taper. The Cross-Section is specified as a ggcylinder, the Cross Section is circular. The xscale and yscale are specified via tables.

 # /usr/local/gd1/examples-from-the-manual/zxscale-example.gdf

 define(R1, 1 )
 define(R3, 3 )

 define(DR, 0.1*R1)

 -general
    outfile= /tmp/UserName/bla
    scratch= /tmp/UserName/scratch-

 -mesh
    spacing= R1 / 10
    pxlow=  -16, pxhigh= 5
    pylow = -(R3+DR), pyhigh= R3+DR
    pzlow = -(R3+DR), pzhigh= R3+DR

 # Compile the program which creates the Table.
 system( $FC Two-Cosine-Table.f90 )
 # Run the program which creates the table.
 system( ./a.out >  Two+Cosine-Table )

# The source Code looks like:
#    Pi= 4*ATAN(1.0)
#    z0= 0
#    zN= 10
#    N= 100
#    DO i= 1, N
#       z= z0 + (i-1)*(zN-z0) / (N-1)
#       WRITE (*,*) z, 2 - COS((z-z0) * Pi/(zN-z0))
#    END DO
#    END
#

##
## Create the tapered Beampipe.
##
 -ggcylinder
    material= 3
    origin= ( 0, 0, 0 )
    xprime= ( 0, 0, 1 )  # The x'-Direction.
    yprime= ( 0, 1, 0 )  # The y'-Direction.
                         # The z'-Direction is then implicitely the
                         # ( -1, 0, 0 ) Direction.
                         #    z' = x' cross y'
    range= ( -3, 14 )  # The Range of the z'-Values.

    # Filenames of the Tables.
    zxscale= Two+Cosine-Table
  ##  zyscale= -none-

    clear  # Clear any old Polygon-Description of the Footprint.
    #
    # This decribes a circular Footprint.
    #
     # point= (x', y')
    point= ( 0, -R1 )
      arc, radius= R1, type= clockwise, size= small
    point= ( 0,  R1 )
      arc
    point= ( 0, -R1 )
 # show= now
    doit

 -volumeplot, scale= 4, doit

**Figure 1.20:** The Discretisation of a Cosine-Taper, specified as a ggcylinder with zxscale.
$\begin{figure}\centerline{ \psfig{figure=zxscale-example.ps,width=18cm,bbllx=-2pt,bblly=-2pt,bburx=716pt,bbury=556pt,clip=} }\end{figure}$

-gbor: A general Body of Revolution in general Direction

A gbor is a Body of Revolution with a Cross Section described as a general Polygon. This Cross Section is swept around some Axis in a general Direction. Moreover, only Volume that fulfills some additional Condition will be filled.

 ##############################################################################
 # Flags: nomenu, noprompt, nomessage,                                        #
 ##############################################################################
 # section -gbor                                                              #
 ##############################################################################
 # material       =  1                                                        #
 # whichcells     = all, taboo= none                                          #
 #     show       = off                 -- (off | all | later | now)          #
 #     name       = gbor-000000000                                            #
 # inside         = yes                 -- (yes|no)                           #
 # originprime    = ( 0.0, 0.0, 0.0 )                                         #
 # zprimedirection= ( 0.0, 0.0, 1.0 )                                         #
 # rprimedirection= ( 1.0, 0.0, 0.0 )                                         #
 # range          = ( 0.0, 360.0 )                                            #
 # xscaleprime    = 1.0                 -- Elliptic Coordinates.              #
 # yscaleprime    = 1.0                 -- Elliptic Coordinates.              #
 ##############################################################################
 ## Syntax:                                                                   #
 #  point= (Zi, Ri)                                                           #
 #  arc, radius= RADIUS, type= [clockwise | counterclockwise]                 #
 #       size= [small | large ]                                               #
 #       deltaphi= 5                                                          #
 #  ellipse, center= (Z0, R0), size= [small | large ]                         #
 #       deltaphi= 5                                                          #
 ##############################################################################
 # doit, return, help, list, reset, clear                                     #
 ##############################################################################

material= MAT:
The Material Index that shall be assigned to the Volume.
whichcells
Possible Values are all, or a Material-index.
If whichcells=all, all Volume inside the gbor is assigned the Material-index, provided the former Material is not taboo. If whichcells is a Material-index, only the Parts of the gbor that are currently filled with the given Index are assigned the new Material-Index.
taboo
Possible Values are none, or a Material-index.
If taboo=none, all Volume inside the gbor is assigned the Material-index. If taboo is a Material-index, only the Parts of the gbor that are currently filled with another Index than the given Index are assigned the new Material-Index.
originprime:
The Coordinates of the Origin of the gbor.
zprimedirection:
The Direction of the z'-axis of the gbor.
rprimedirection:
The Direction of the r'-Vector of the Polygon. The r'-Direction will internally be enforced to be perpendicular to the z'-Direction.
range:
Start and End Values (in Degrees) of the phi-Coordinate of the Body of Revolution.
xscaleprime, yscaleprime:
The x'-Coordinates, resp. y'-Coordinates of the Footprint are multiplied by these Factors.
inside:
Flag, specifying whether the Volume inside the gbor shall be assigned the Material Index MAT, or whether the Volume outside of it shall be set to the Material Index MAT.
show:
Flag, specifying whether an Outline of the specified gbor shall be displayed.
If show=off, no Outline will be displayed.
If show=later, the Outline of the gbor will be shown later, together with Outlines of other specified Items. If show=all is present, the Outlines of all other specified Items bricks gccylinders, ggcylinders and gbors found in the Inputstream so far where show was not off will be displayed.
point= (XI, YI):
XI, YI are the Coordinates of the i.th Point in the Polygon that describes the Polygon of the gbor. There have to be minimum 3 Points, or 2 Points and an Arc or 2 Points and an Ellipse.
arc:
(optional):
Indication, that there shall be a circular Arc from the Point that was specified before, to the Point that will be specified as the next Point.
In Order to determine the Arc between two Points, three Parameters are necessary: The Radius of the Arc, whether the Connection is Clockwise or Counterclockwise, and whether the Connection shall take the large Path or the small Path.
- radius= RADIUS:
  The Points are to be connected by an Arc with Radius=RADIUS
- size= [small | large] (optional):
  Indication, whether the Connection between the two Points shall be on the smaller or the larger Side of the Arc.
- type= [clockwise | counterclockwise]:
  Indication, whether the Connection between the two Points shall proceed Clockwise or Counterclockwise along the Arc.
- deltaphi:
  The wanted Resolution of the Arc or Ellipse in Degrees. A circular Arc or a Part of an Ellipse is internally discretised as a Polygon. The deltaphi Parameter controls the Resolution of that Discretisation.
clear:
Clears the current Polygon Path.
doit:
Puts the current Data as the Data of a General Body of Revolution into the meshing Database.

Example The following describes something like a Tuning-Plunger.

 # /usr/local/gd1/examples-from-the-manual/plunger0.gdf

 define(PlungerInnerRadius, 100e-3/2 )
 define(PlungerCurvature, 16e-3 )
 define(PlungerAngle, -67.5*@pi/180 )

 -general
    outfile= /tmp/UserName/example
    scratch= /tmp/UserName/scratch-

    text()= A Plunger, modelled as a body of revolution.
    text()= Curvature     : PlungerCurvature
    text()= Radius        : PlungerInnerRadius
    text()= Angle of Axis : eval(PlungerAngle * 180 / @pi) Degrees

 -mesh
    spacing= 0.2e-2
    pxlow= -0.12, pxhigh= 0.05
    pylow= -0.02, pyhigh= 0.18
    pzlow= -6e-2, pzhigh= 6e-2

 -gbor
     material= 4
     originprime= ( 0, 0, 0 )
     zprimedirection= ( cos(PlungerAngle), sin(PlungerAngle), 0 )
     rprimedirection= ( 0, 0, 1 )
     range= ( 0, 360 )

     clear
        # point= ( z, r )
     point= ( 0, 0 )
     point= ( 0, PlungerInnerRadius-PlungerCurvature )
        arc, radius= PlungerCurvature, size= small, type= counterclockwise
     point= ( -PlungerCurvature, PlungerInnerRadius )
     point= ( -170e-3, PlungerInnerRadius )
     point= ( -170e-3, 0 )
# show= now
     doit

 -volumeplot, eyeposition= ( 1, -0.5, 0.6 )
     scale= 3
     doit

**Figure 1.21:** A simple gbor.
$\begin{figure}\centerline{ \psfig{figure=gbor-example0.ps,width=18cm,bbllx=-2pt,bblly=-2pt,bburx=716pt,bbury=556pt,clip=} }\end{figure}$

Example The following discretises the Connection of two circular Waveguides, meeting at an Angle of 90 Degrees.

 # /usr/local/gd1/examples-from-the-manual/gbor-example1.gdf
define(LargeNumber, 10000)       # some big number

define(MAXCELLS, 1e+5)

define(XLOW, 0) define(XHIGH, 5e-2)
define(YLOW, 0) define(YHIGH, 6e-2)
define(ZLOW, -1.1e-2) define(ZHIGH, 0)

define(STPSZE, ((XHIGH-XLOW)*(YHIGH-YLOW)*(ZHIGH-ZLOW)/MAXCELLS)**(1/3) )

 -mesh
    volume= ( XLOW, XHIGH, \
              YLOW, YHIGH, \
              ZLOW, ZHIGH )

    spacing= STPSZE

 -general
    outfile= /tmp/UserName/example
    scratch= /tmp/UserName/scratch
 define(R, 1.0e-2)
    text()= Intersection of two circular Cylinders with Radius R
    text()= generated as general Cylinders
    text()= where 'taboo' is specified.
    text()= stpsze= STPSZE, maxcells= MAXCELLS

#
# Fill the Universe with Metal.
#
 -brick
    material= 1
    volume= ( -LargeNumber, LargeNumber, \
              -LargeNumber, LargeNumber, \
              -LargeNumber, LargeNumber )
    doit

#
# First Step,
# fill Cells above the Diagonal with Material 3.
# these Cells will not be filled by the first circular Cylinder,
# since we will specify 'taboo= 3'.
#
#
 -ggcylinder
    material= 3,
    origin= ( 0, 0, 0 ), xprime= ( 1, 0, 0 ), yprime= ( 0, 1, 0 ),
    range= ( ZLOW, ZHIGH ),

    clear
    point= ( XLOW, YLOW ), point= ( XLOW, YHIGH ),
    point= ( XLOW+(YHIGH-YLOW), YLOW )

    doit

#
# Second Step:
# Fill a circular Cylinder in x-Direction,
# but NOT Cells with Material Index 3 (taboo=3).
#
 -ggcylinder
    material= 0, taboo= 3,
    xprime= ( 0, 1, 0 ), yprime= ( 0, 0, 1 ),  # So the Axis will be in +x.
    origin= ( 0, 4e-2, 0 ),                    # Shift of Origin.
    range= ( XLOW, XHIGH ),

    clear
       point= ( -R, 0 ),
         arc, radius= R, type= counterclockwise,
       point= ( 0, -R ),
         arc, radius= R,
       point= ( R, 0 ),
    doit

#
# Third Step:
# Fill a circular Cylinder in y-Direction,
# but ONLY Cells with Material Index 3 (whichcells=3).
#
 -ggcylinder
    material= 0, whichcells= 3, taboo= none
    xprime= ( 1, 0, 0 ), yprime= ( 0, 0, -1 ),  # So the Axis will be in +y.
    origin= ( 2.e-2, 0, 0 ),                    # Shift of Origin.
    range= ( YLOW, YHIGH ),

    clear
       point= ( -R, 0 ),
          arc, radius= R, type= clockwise,
       point= ( 0, R ),
          arc, radius= R,
       point= ( R, 0 ),
    doit

 -volumeplot
    eyeposition= ( 1, 2, 1 )
    scale= 3.5
    doit

**Figure 1.22:** The Intersection of two circular Cylinders, where **whichcells** and **taboo** were specified.
$\begin{figure}\centerline{ \psfig{figure=gbor-example1.ps,width=18cm,bbllx=-2pt,bblly=-2pt,bburx=716pt,bbury=556pt,clip=} }\end{figure}$

Example The following describes a reentrant Cavity.

 # /usr/local/gd1/examples-from-the-manual/gbor-example.gdf
 define(MaxCells, 2e+6)

 #
 # define the geometry parameters
 #
 define(RBeamTube, 4.7625e-2)
 define(RCurve,  1.0e-2)
 define(ZGapNose, 10.9e-2)
 define(RLarge, 25.0e-2)  define(RSmall, 15.0e-2)  define(RCenter, 10.0e-2)

 define(INF, 10000) define(EL, 1) define(MAG, 2)

 define(XLOW, -0.250) define(XHIGH, 0.250)
 define(YLOW, -0.250) define(YHIGH, 0.250)
 define(ZLOW, -0.200) define(ZHIGH, 0.200)

 define(STPSZE, ((XHIGH-XLOW)*(YHIGH-YLOW)*(ZHIGH-ZLOW)/MaxCells)**(1/3) )

 #
 # gdfidl can evaluate sin(), cos(), atan() and X**Y
 # definition of functions degsin() and degcos()
 #
 sdefine(degsin, [sin((@arg1)*@pi/180)])
 sdefine(degcos, [cos((@arg1)*@pi/180)])
 sdefine(degtan, [sin((@arg1)*@pi/180)/cos((@arg1)*@pi/180)])

-general
   outfile= /tmp/UserName/example
   scratch= /tmp/UserName/scratch-

   text(3)= A Quarter of a reentrant Cavity.
   text()= The Cavity is described as a Body of Revolution.
   text()=
   text()= maxcells= MaxCells, stpsze= STPSZE

-mesh
   pxlow= 0*XLOW, pxhigh= 1*XHIGH
   pylow= 0*YLOW, pyhigh= 1*YHIGH
   pzlow= 1*ZLOW, pzhigh= 1*ZHIGH

   cxlow= mag, cxhigh= mag
   cylow= mag, cyhigh= mag
   czlow= ele, czhigh= ele

   spacing= STPSZE

 -material
   material= 3, type= electric

 -brick
    #
    # We fill the Universe with Metal.
    #
    material= 3
       volume= ( -INF,INF, -INF,INF, -INF,INF )
    doit

 #
 # We carve out the Cavity.
 #
 -gbor
     material= 0, range= ( 0, 360 )
     origin= ( 0, 0, 0 )
     show= later,      # Do not show now, but show later.

     clear   # Clear a previous Polygon List.
        point= (     0          , 0 ),
        point= ( ZHIGH+2*STPSZE , 0 ),
        point= ( ZHIGH+2*STPSZE , RBeamTube ),
        point= ( ZGapNose+RCurve, RBeamTube ),
           arc, radius= RCurve, size= small, type= clockwise,
           deltaphi= 10
define(rdum, RBeamTube+(1+degcos(30))*RCurve)
define(zdum, ZGapNose +(1-degsin(30))*RCurve)
        point= ( zdum, rdum )
define(deltaz, RSmall-zdum)
define(deltar, deltaz*degtan(30))
 define(ffac, 0.85)   ## adjust this for a smooth transition
define(zdum2, zdum+ffac*deltaz)
define(rdum2, rdum+ffac*deltar)
        point= ( zdum2, rdum2 )
          arc, radius= RCurve, size= small, type= counterclockwise,
          deltaphi 10
        point= ( RSmall, RCenter-0.8*RCurve ),
        point= ( RSmall, RCenter ),
           arc, radius= RSmall, size= small, type= counterclockwise,
           delta= 3
        point= ( -RSmall, RCenter ),
        point= ( -RSmall, RCenter-0.8*RCurve ),
           arc, radius= RCurve, size= small, type= counterclockwise,
           deltaphi= 10
        point= ( -zdum2, rdum2 )
        point= ( -zdum, rdum )
           arc, radius= RCurve, size= small, type= clockwise, delta 10
        point= ( -(ZGapNose+RCurve), RBeamTube ),

        point= ( ZLOW-2*STPSZE, RBeamTube ),
        point= ( ZLOW-2*STPSZE, 0 )
     list
     doit
#
# Enforce some Meshplanes:
#
-mesh
   zfixed( 2, -(ZGapNose+RCurve), -ZGapNose ) # At the Noses.
   zfixed( 2,  (ZGapNose+RCurve),  ZGapNose ) # At the Noses.

   zfixed( 2, -RSmall, RSmall)                # At the z-Borders of the Cavity.

-volumeplot
   scale= 3
   doit

**Figure 1.23:** A complicated gbor
$\begin{figure}\centerline{ \psfig{figure=gbor-example.ps,width=18cm,bbllx=-2pt,bblly=-2pt,bburx=716pt,bbury=556pt,clip=} }\end{figure}$

Example The following describes two Bodies of Revolution that look similiar to Glasses. The Shape is only specified once, but two different Glasses are generated by varying 'zprime' and 'rprime'

 # /usr/local/gd1/examples-from-the-manual/gbor-glasses.gdf

define(MAXCELLS,1e+6)

define(XLOW,-5e-2) define(XHIGH,18e-2)
define(YLOW,-0e-2) define(YHIGH,17e-2)
define(ZLOW,-3e-2) define(ZHIGH,18e-2)
define(STPSZE, ((XHIGH-XLOW)*(YHIGH-YLOW)*(ZHIGH-ZLOW)/MAXCELLS)**(1/3) )

 -general
    outfile= /tmp/UserName/glasses
    scratch= /tmp/UserName/glasses-scratch-

 -mesh
    spacing= STPSZE
    volume= ( XLOW, XHIGH, \
              YLOW, YHIGH, \
              ZLOW, ZHIGH )

# Fill the Universe with Vacuum.
 define(LargeNumber,10000)
 -brick
     material= 0
        volume= ( -LargeNumber, LargeNumber, \
                  -LargeNumber, LargeNumber, \
                  -LargeNumber, LargeNumber )
     doit

 #
 # The Glasses:
 #
  -gbor

     #
     # Definition of the Cross-Section:
     #
     clear
     point= (  0.7e-2,      0 ),
     point= (       0, 4.0e-2 ),
       arc, radius=0.25e-2, size= large, type= clockwise
     point= (  0.3e-2, 4.0e-2 ),
     point= (  1.0e-2, 1.0e-2 ),
     point= (  8.0e-2, 0.8e-2 ),
     point= ( 10.0e-2, 1.4e-2 ),
     point= ( 15.0e-2, 6.0e-2 ),
       arc, radius= 0.4e-2, type= clockwise
     point= ( 15.2e-2, 5.4e-2 ),
     point= ( 10.0e-2,      0 )

     #
     # That Cross-Section is used twice,
     # with different Parameters for origin, zprime etc..
     #

     material= 1,
     origin= ( -2e-2, 0, 4e-2 ),
     zprimedir= ( 1, 0, 0 ),
     rprimedir= ( 0, 1, 0 ),
     range= ( -90, 90 ),
 ##    show= now
     doit                 # This 'doit' generates the first 'glass'.


     material= 3
     origin= ( 0, 12e-2, 4e-2 ),
     zprimedir= ( 1, -0.5, 0.7 ),
     rprimedir= ( 0, 1, 0 ),
     range= ( 0, 360 ),
 ##    show= all
     doit                 # This 'doit' generates the second 'glass'

 -volumeplot
     eyeposition= ( 0.7, 1, 0.5 )
     scale= 4
    doit

**Figure 1.24:** Two complicated gbors (Glasses).
$\begin{figure}\centerline{ \psfig{figure=gbor-glasses.ps,width=18cm,bbllx=-2pt,bblly=-2pt,bburx=716pt,bbury=556pt,clip=} }\end{figure}$

-stlfile: CAD Import via STL-File

This Section is about importing a Geometry Description from a CAD System^1.3 via a STL-file (STereo-Lithography). A STL-file describes a closed Body via a Set of Triangles.

The so described Body can be rotated, shrunk or expanded and shifted.

 ##############################################################################
 # Flags: nomenu, noprompt, nomessage,                                        #
 ##############################################################################
 # section -stlfile                                                           #
 ##############################################################################
 # file= /usr/local/gd1/examples/woman.stl                                    #
 # material  =  1                                                             #
 # whichcells= all, taboo= none, nboundaries=  1                              #
 # originprime    = ( 0.0, 0.0, 0.0 )                                         #
 # xprimedirection= ( 1.0, 0.0, 0.0 )                                         #
 # yprimedirection= ( 0.0, 1.0, 0.0 )                                         #
 # xscale= 1.0                                                                #
 # yscale= 1.0                                                                #
 # zscale= 1.0                                                                #
 # debend = no                          -- debend Description around uAxis    #
 #    uaxis= z                          -- [xyz] : Direction of debend-Axis   #
 #    radius= 0.0                                                             #
 #    v0    = 0.0                       -- v0, w0: Coordinates of the Axis.   #
 #    w0    = 0.0                                                             #
 # show   = no                          -- ( yes | no )                       #
 #    plotbbox= ( -1.0e+30, 1.0e+30,  \                                       #
 #                -1.0e+30, 1.0e+30,  \                                       #
 #                -1.0e+30, 1.0e+30 )                                         #
 # ----- Fixed Planes from Analysis of Patches Normals:                       #
 # xfixed= no                           -- ( yes | no )                       #
 #     dx= auto                         -- Treshold                           #
 #    xda= auto                         -- Treshold                           #
 # yfixed= no                           -- ( yes | no )                       #
 #     dy= auto                         -- Treshold                           #
 #    yda= auto                         -- Treshold                           #
 # zfixed= no                           -- ( yes | no )                       #
 #     dz= auto                         -- Treshold                           #
 #    zda= auto                         -- Treshold                           #
 ##############################################################################
 # doit, return, help                                                         #
 ##############################################################################

file= NAME_OF_STLFILE:
The name of the STL-File (in ASCII) that shall be imported.
material= MAT:
The Material Index that shall be assigned to the described Volume.
whichcells
Possible Values are all, or a Material-Index.
If whichcells=all, all Volume inside the STL-Body is assigned the Material-Index, provided the former Material is not taboo. If whichcells is a Material-Index, only the Parts of the STL-Body that are currently filled with the given Index are assigned the new Material-Index.
taboo
Possible Values are none, or a Material-Index.
If taboo=none, all Volume inside the STL-Body is assigned the Material-Index. If taboo is a Material-Index, only the Parts of the STL-Body that are currently filled with another Index than the given Index are assigned the new Material-Index.
nboundaries= [1,2]
Specifies what Number of Boundaries must be crossed, to consider a Point being inside the Body.
debend= [yes|no]
The Body which is described by the STL-File can be de-bended. To de-bend, one has to specify around what Axis the Body originally was bend, and what the bending Radius is.
uaxis= [x|y|z]
Parameter for debend=yes. The Axis around which the Body is bended.
radius= NUMBER
Parameter for debend=yes. The bending Radius.
v0= NUMBER, w0= NUMBER
Parameters for debend=yes. The Coordinates of the bending Axis.
originprime= (X0, Y0, Z0):
xprimedirection= (XXN, XYN, XZN):
yprimedirection= (YXN, YYN, YZN):
xscale= XS, yscale= YS, zscale= ZS:
The Coordinates of the STL-Data are transformed as follows: A 3x3 matrix (A) is built, such that A11, A21, A31 are the Components of the normalised "xprimedirection". The Direction "yprimedirection" is enforced to be perpendicular to "xprimedirection". The Result is normalised and taken as the second Column of (A). The third Column of (A) is the normalised Cross Product of "xprimedirection" and "yprimedirection". (The Matrix (A) is a rotation Matrix.)
The Coordinates of a Point P of the STL-set are now transformed via
```
 
            P <= (A) * P
            P_x <= P_x * xscale + X0
            P_y <= P_y * yscale + Y0
            P_z <= P_z * zscale + Z0
```
show= [yes|no] :
Flag, specifying whether a Plot of the transformed triangles shall be shown.
plotbbox= (X0,X1, Y0,Y1, Z0,Z1) :
If show=yes, ie. when a Plot of the read Triangles is done, only the Triangles within these Borders are shown.
xfixed= [yes|no], yfixed= [yes|no], zfixed= [yes|no] :
If xfixed=yes, the Triangles are analysed and fixed Meshplanes are inserted where a significant Fraction of Triangles with Plane-Normal in x-Direction are.
yfixed=yes: The Corresponding for y-directed Plane-Normals. zfixed=yes: The Corresponding for z-directed Plane-Normals.
doit:
Puts the current Data as the Data of a STL-Set into the meshing Database.

Example

 # /usr/local/gd1/examples-from-the-manual/stl-example2.gdf

 -mesh
     spacing= 1
     volume= ( 0,200, 0,130, -200,0 )

 -stlfile
     file= /usr/local/gd1/examples/wagner60kASTL.stl
     xprime= ( 1, 0, 0 )
     yprime= ( 0, 0, -1 )
     material= 1, taboo= none
##     show= yes,
     doit

 -volumeplot, scale= 2.5, eyepos= ( 1, 2, 0.5), doit

**Figure 1.25:** A discretisation of a Wagner Bust, described as a STL-file.
$\begin{figure}\centerline{ \psfig{figure=stl-example2.ps,width=18cm,bbllx=-2pt,bblly=-2pt,bburx=716pt,bbury=556pt,clip=} }\end{figure}$

Example

 # /usr/local/gd1/examples-from-the-manual/stl-example-debend.gdf
 
 define(FILE, dipchamSTL00)
 define(INF, 10000)

 define(SIGMA, 10e-3)
 define(STPSZE, SIGMA/5 )
 define(TRAILER, 68*SIGMA)
 define(OFFSET,20e-3)

 define(A,    300.0e-3)
 define(B,    400.0e-3)

 define(ZYL1, 120e-3)

###############################################################

 -general
   outfile= /tmp/UserName/bla
   scratch= /tmp/UserName/scratch-
   text()= stpsze= STPSZE
   text()= sigma= SIGMA, sigma/stpsze= eval(SIGMA/STPSZE)
   text()= charge= CHARGE, RDV
   text()= offset= OFFSET	

###############################################################         
 -mesh
   pxlow= -ZYL1+40e-3, pxhigh= ZYL1+100e-3
   pylow= -ZYL1,     pyhigh= ZYL1
   pzlow= 2e-3,     pzhigh= 398e-3
   pzhigh= 1.59

   spacing= STPSZE

#########################################################################
-material
  material= 3, type= electric

-brick
  #
  # Fill the universe with metal.
  #
  material= 1, name= Background
     volume= (-INF,INF, -INF,INF, -INF,INF)
  doit
################################################################

-stlfile
   file= /usr/local/gd1/examples-from-the-manual/DP_VAC_Xapa.stl
   material= 0, whichcells= all, taboo= none
    #
    # The stl-file does not describe the volume filled with vacuum,
    # but the metal body.
    # To model the vacuum part, we use a trick:
    # We say that the number of triangles that are to be crossed
    # when going from inside the body to outside of the body
    # (to infinity) has to be a multiple of two.
    #
   nboundaries= 2

# define(UA, 1)
 define(UA, 2)
# define(UA, 3)
   if (UA == 2) then
      originprime = ( 0, 0, -6093e-3 )
      xprimedirection= ( 0, 0, 1 )
      yprimedirection= ( 1, 0, 0 ) # axis= +y
   elseif (UA == 1) then
      originprime = ( 0, -6093e-3, 0 )
      xprimedirection= ( 0, 1, 0 )
      yprimedirection= ( 1, 0, 0 ) # axis= -z
   else
      originprime=  ( 0, -6093e-3, 0 )
      xprimedirection= ( 0, 1, 0 )
      yprimedirection= ( 0, 0, 1 ) # axix= +x
   end if
   xscale= 1e-3
   yscale= 1e-3
   zscale= 1e-3
   if (1) then
      #
      # The geometry is a dipole chamber.
      # The charge in reality travels over a circular path.
      # As GdfidL can only compute wakepotentials when the
      # exciting charge and the witness charges are traveling
      # in + z-direction, we de-bend the geometry such that the
      # originaly arc-like beampipe is straight.
      #
      debend= yes
      if (UA == 2) then
         uaxis= y # (u,v,w) = (y,z,x)
         radius= 8.25
         v0= 0
         w0= -8.25
      elseif (UA == 1) then
         uaxis= z # (u,v,w) = (z,x,y)
         radius= 8.25
         v0= -8.25
         w0= 0
      else
         uaxis= x # (u,v,w)= (x,y,z)
         radius= 8.25
         v0= 0
         w0= -8.25
      end if
   end if
   
##   show= yes
   doit

#########################################################################
-volumeplot
      scale= 4
  roty= 90
  bbylow= 0.
      doit
# end

##########################################################################

#
# Wake-Parameters.
#
 -fdtd
  -ports
    name= lower_end, plane= zlow,   modes= 0, npml= 20, doit
    name= upper_end, plane= zhigh,  modes= 0, npml= 20, doit

 -lcharge 
    xpos    = OFFSET
    ypos    = 0
    charge  = 1e-12
    sigma   = SIGMA
    shigh   = 12*SIGMA +TRAILER
##    showdata= yes

# -fdtd, doit

**Figure 1.26:** A Discretisation of a Dipole Chamber. The Arc-like Beam-Pipe has been de-bended to allow the Computation of Wakepotentials.
$\begin{figure}\centerline{ \psfig{figure=stl-example-debend.ps,width=18cm,bbllx=-2pt,bblly=-2pt,bburx=716pt,bbury=556pt,clip=} } \end{figure}$

-geofunction: Analytic Description

This Section allows the Specification of the Parameters of an analytic Function which describes a Body. The analytic Function must be programmed in some external Binary which is loaded at run Time.

 ##############################################################################
 # Flags: nomenu, noprompt, nomessage,                                        #
 ##############################################################################
 # section -geofunction                                                       #
 ##############################################################################
 # material  =  1                                                             #
 # whichcells= all, taboo= none                                               #
 # fdescriptionsubroutine=-none-
 # a1= 0.0,                             b1= 0.0                               #
 # a2= 0.0,                             b2= 0.0                               #
 # a3= 0.0,                             b3= 0.0                               #
 # a4= 0.0,                             b4= 0.0                               #
 # a5= 0.0,                             b5= 0.0                               #
 # a6= 0.0,                             b6= 0.0                               #
 # a7= 0.0,                             b7= 0.0                               #
 # a8= 0.0,                             b8= 0.0                               #
 # a9= 0.0,                             b9= 0.0                               #
 ##############################################################################
 # doit, return, help                                                         #
 ##############################################################################

material:
The Material to use.
whichcells:
Specifies what Areas are to be filled with "material". If "whichcells= all", everything within the Volume is filled. If "whichcells= N", only Space that is currently filled with Material N, and which is within the Volume is filled.
taboo= [none|0..50]:
Specifies Volumes NOT to be filled with Material. If "taboo= none", all Volume within will be filled with "material". If "taboo= N", only Volume that is already filled with Material N and is within the Volume is filled.
fdescriptionsubroutine= NAME-OF-A-SHARED-OBJECT:
The Name of the shared Object that contains a SUBROUTINE which computes whether a Point is in the Body or not. The Subroutine must have the Name fgeosub and has to have a declaration like
```
 SUBROUTINE fgeosub( Point, AArray, IsIn )
 DOUBLE PRECISION, INTENT(IN), DIMENSION(1:3)  :: Point
 DOUBLE PRECISION, INTENT(IN), DIMENSION(1:20) :: AArray
 INTEGER,          INTENT(INOUT) :: In
```
The Point Parameter are the cartesian Components of the Point, the AArray Parameter are the numbers a1..a9, b1..b9, and the IsIn Parameter is to be computed. It shall be Zero, if the Point is NOT in the Body.
doit:
The Parameters of the geofunction are put into the Database, and the shared Object is loaded.

Example

 # /usr/local/gd1/examples-from-the-manual/geofunction-example.gdf
 -general
    outfile= /tmp/UserName/geofunction
    scratch= /tmp/UserName/scratch

 -mesh
    spacing= 0.02e-3
    pxlow= -3e-3, pxhigh= 3e-3
    pylow= -3e-3, pyhigh= 3e-3
    pzlow= 0, pzhigh= 5e-3
  czlow= magnetic, czhigh= magnetic
  pylow= 0, cylow= magnetic

 -brick
    material= 0, whichcells= all, taboo= none
    volume= ( -INF,INF, -INF,INF, -INF,INF )
    doit

    # Fill Parts of the Universe which shall later be described
    # by the 'geofunction'.
 -brick
    material= 10
    xlow= -1e-3, xhigh= 1e-3
    ylow= -INF, yhigh= INF
    zlow= -INF, zhigh= INF
  sloppy= yes
    doit
    xlow= -INF, xhigh= INF
    ylow= -1e-3, yhigh= 1e-3
    doit
  sloppy= no

 system( ifort -O3 -fPIC -auto -c \
            ./PointInsideFunction.f90 )
 system( gcc -fPIC -shared -Wl,-soname,PointInsideFunction.so \
           -o /tmp/PointInsideFunction.so PointInsideFunction.o )
    
 define(VAL, 1)
 -geofunction
    #
    # If this Inputfile is to be used with PVM/MPI,
    # each Task will try to load the Shared Object.
    # We assume here, /tmp/ is accessible by each Task.
    #
    fdescriptionsubroutine= /tmp/PointInsideFunction.so
    material= 3, whichcells= 10, taboo= none
## whichcells= all
    a1= 1              # Key
    a2= 1825283, a3= 692618, a4= 0.7 * 3.28e-3, a5= 0,
    a8= 1              # Key: Pot gt val
    a9= VAL            # Aequipotential-Value
   doit

    material= 4
    a8= -1              # Key Pot lt val
    a9= -VAL            # Aequipotential-Value
   doit

 -brick, material= 0, whichcells= 10
         volume= ( -INF,INF, -INF,INF, -INF,INF ), doit

 -material
    material= 3, type= electric
    material= 4, type= electric
    material= 10, type= electric

 -volumeplot, scale= 4, eyepos ( -1, -2, 3 ), doit

 -eigenvalues
    estimation= 100e9
#    doit

The Sourcecode PointInsideFunction.f90:

 
 SUBROUTINE fgeosub( Point, A, In )
 
 DOUBLE PRECISION, INTENT(IN), DIMENSION(1:3)  :: Point
 DOUBLE PRECISION, INTENT(IN), DIMENSION(1:20) :: A
 INTEGER,          INTENT(INOUT) :: In
 
 DOUBLE PRECISION :: Pi, Phi, P
 DOUBLE PRECISION :: x, y, z, z0, z1, zz, az, rmz, oodL, a01, a10

    Pi= 4*ATAN(1.0d0)

    IF (NINT(A(1)) == 1) THEN
       x= Point(1)
       y= Point(2)
       z= Point(3)
       P = A(4)+A(5)*z
       Phi= A(2)*(x**2-y**2) &
          + A(3)*(x**2+y**2+(P/Pi)**2)*wbCos(2*Pi*z/P)

       IF (A(8) > 0) THEN
          IF (Phi > A(9)) THEN
             In= 1
          ELSE
             In= 0
          END IF
       ELSE
          IF (Phi < A(9)) THEN
             In= 1
          ELSE
             In= 0
          END IF
       END IF
    ELSE IF (NINT(A(1)) == 2) THEN
 
! a1,a2,a3,a4,a5,a6,a7,a8,a9 => A( 1: 9)
! b1,b2,b3,b4,b5,b6,b7,b8,b9 => A(11:19)
 
!      Period described as a Polinomial
!      Amplitude described as a Polinomial
 
       x= Point(1)
       y= Point(2)
       z= Point(3)
       z0= A(2)
       z1= A(3)
!c      write (*,*) ' a(1:9):', a(1:9)
!c      write (*,*) ' a(11:19):', a(11:19)
       IF ((z < z0) .OR. (z > z1)) THEN
          In= 0
          RETURN
       END IF
       zz= z-z0
       oodL= 1 / (z1-z0)
       P = A(4) +zz*(A(5)-A(4))*oodL
       az= A(6) +zz*(A(7)-A(6))*oodL
       rmz= A(8)+zz*(A(9)-A(8))*oodL
       a10= (rmz**2-1) &
          / (2*(rmz*az)**2+(rmz**2+1)*(P/Pi)**2)
       a01= ((rmz**2+1)*az**2+2*(P/Pi)**2) &
          / (2*(rmz*az)**2+(rmz**2+1)*(P/Pi)**2) &
          / az**2
       Phi= a01*(x**2-y**2) &
          + a10*(x**2+y**2+(P/Pi)**2)*wbCos(2*Pi*zz/P)

       IF (A(11) > 0) THEN
          IF (Phi > A(12)) THEN
             In= 1
          ELSE
             In= 0
          END IF
       ELSE
          IF (Phi < A(12)) THEN
             In= 1
          ELSE
             In= 0
          END IF
       END IF
 
    ELSE
       In= 0
    END IF

 CONTAINS

    DOUBLE PRECISION FUNCTION wbCos( x )
    DOUBLE PRECISION, INTENT(IN) :: x

    DOUBLE PRECISION :: xx
    INTEGER :: iSign

       xx= ABS(x)
       DO WHILE (xx > 2*Pi)
          xx= xx - 2*Pi
       END DO

       IF (xx > Pi) THEN
          iSign= -1
          xx= xx - Pi
       ELSE
          iSign= 1
       END IF

       IF (xx > Pi/2) THEN
          iSign= -iSign
          xx= Pi - xx
       END IF


       wbCos= iSign* &
           (1 - xx**2/2 + xx**4/(2*3*4) - xx**6 / (2.*3.*4.*5.*6.) )
       !!       + xx**8 / (2.*3.*4.*5.*6.*7.*8.) &
       !!       - xx**10 / (2.d0*3.d0*4.d0*5.d0*6.d0*7.d0*8.d0*9.d0*10.d0) )

    END FUNCTION wbCos

 END SUBROUTINE fgeosub

**Figure 1.27:** Part of a RF-Quadrupole, where the Electrodes are described by an Algorithm.
$\begin{figure}\begin{center}\quad \quad \psfig{figure=geofunction-example.ps,wi... ...m,bbllx=-2pt,bblly=-2pt,bburx=716pt,bbury=556pt,clip=} \end{center} \end{figure}$

-transform: Rotations, Translations

All geometric Items are transformed by a Transformation Matrix. Initially, that Transformation Matrix is the unity Matrix. The Specification of a Translation or Rotation modifies the transformation Matrix accordingly. The Transformations are applied one after the other.

 ##############################################################################
 # Flags: nomenu, noprompt, nomessage,                                        #
 ##############################################################################
 # Section: -transform                                                        #
 ##############################################################################
 # -translate                                                                 #
 # -rotate                                                                    #
 #                                                                            #
 # Matrix:                                                                    #
 #     1.00000000    ,    0.00000000    ,    0.00000000    ,    0.00000000    #
 #     0.00000000    ,    1.00000000    ,    0.00000000    ,    0.00000000    #
 #     0.00000000    ,    0.00000000    ,    1.00000000    ,    0.00000000    #
 #     0.00000000    ,    0.00000000    ,    0.00000000    ,    1.00000000    #
 ##############################################################################
 # reset, ?, return, help                                                     #
 ##############################################################################

-translate:
Enters the Section to specify the next Translation.
-rotate:
Enters the Section to specify the next Rotation.
reset:
Resets the transformation Matrix to the unity Matrix.

 ##############################################################################
 # Flags: nomenu, noprompt, nomessage,                                        #
 ##############################################################################
 # Section: -translate                                                        #
 ##############################################################################
 # offset= ( 0.0, 0.0, 0.0 )                                                  #
 #                                                                            #
 ##############################################################################
 # doit, ?, return, help                                                      #
 ##############################################################################

offset:
Specifies the X, Y, Z Components of the Offset to be applied.
doit:
The Transformation Matrix is modified such that all subsequent specified geometric Items are translated by the specified Offset.

 ##############################################################################
 # Flags: nomenu, noprompt, nomessage,                                        #
 ##############################################################################
 # Section: -rotate                                                           #
 ##############################################################################
 # axis= ( 0.0, 0.0, 1.0 )                                                    #
 # angle= 90.0                                                                #
 # Matrix:                                                                    #
 #     1.00000000    ,    0.00000000    ,    0.00000000    ,    0.00000000    #
 #     0.00000000    ,    1.00000000    ,    0.00000000    ,    0.00000000    #
 #     0.00000000    ,    0.00000000    ,    1.00000000    ,    0.00000000    #
 #     0.00000000    ,    0.00000000    ,    0.00000000    ,    1.00000000    #
 ##############################################################################
 # doit, ?, return, help                                                      #
 ##############################################################################

axis:
Specifies the X, Y, Z Components of the Axis to rotate around.
angle:
Specifies the Angle in Degrees to rotate.
doit:
The Transformation Matrix is modified such that all subsequent specified geometric Items are rotated by the specified Angle around the specified Axis.

Example

 -general
     outfile= /tmp/UserName/bla
     scratch= /tmp/UserName/scratch

 -mesh
     spacing= 5e-3
     pxlow= -0.4, pxhigh= 0.3
     pylow= -0.3, pyhigh= 0.3
     pzlow= -0.1, pzhigh= 0.4

 -transform, reset

 -brick
     material= 0
     volume= ( -BIG,BIG, -BIG,BIG, -BIG,BIG )
     doit

 #
 # Translate all subsequent Items by (0.1, 0, 0).
 #
 -translate, offset= ( 1/10, 0, 0 ), doit

 -brick
    material= 1
    name= brick1
    xlow= 0, xhigh= 0.1
    ylow= 0, yhigh= 0.2
    zlow= 0, zhigh= 0.3
    doit

 #
 # Additionally to the initial Translation,
 # rotate by 90 Degrees around the (0,0,1)-Axis,
 # then rotate 20 Degrees around the (0,1,0)-Axis,
 #
 -rotate,
     axis= ( 0, 0, 1 ), angle= 90, doit
     axis= ( 0, 1, 1 ), angle= 20, doit

 #
 # Next Brick, most Parameters as the first One,
 # but additionally to the Translation now also rotated.
 #
 -brick, material= 2, name= brick2, doit

 #
 # Next Rotation, same Parameters.
 # Because the Rotations etc are all performed,
 # subsequent Items are translated once and rotated now four times.
 #
 -rotate,
     axis= ( 0, 0, 1 ), angle= 90, doit
     axis= ( 0, 1, 1 ), angle= 20, doit

 # Next Brick, except for 'material', the same Parameters as the previous Brick.
 -brick, material= 3, name= brick3, doit

 -volumeplot, scale= 3, doit

**Figure 1.28:** Discretisation of some Bricks, translated and rotated.
$\begin{figure}\centerline{ \psfig{figure=Transformierte-Bricks.ps,width=18cm,bbllx=-2pt,bblly=-2pt,bburx=716pt,bbury=556pt,clip=} }\end{figure}$

-volumeplot: Shows the resulting Mesh

This Section enables the Generation of the Grid and shows the discretised Material Boundaries as generated from the geometric Primitives specified so far.

 ##############################################################################
 # Flags: nomenu, noprompt, nomessage,                                        #
 ##############################################################################
 # Section: -volumeplot                                                       #
 ##############################################################################
 # onlyplotfile  = no         -- Do not display Plot                          #
 # showlines = no                                                             #
 # text     = yes                                                             #
 # scale    = 1.80                                                            #
 # 2dplotopts = -geometry 690x560+10+10                                       #
 #   plotopts = -geometry 800x668+410+40 -noclip                              #
 # eyeposition  = ( -1.0, -2.30, 0.50 )                                       #
 # bbxlow =    -1.0000e+30, bbylow =    -1.0000e+30, bbzlow =    -1.0000e+30  #
 # bbxhigh=     1.0000e+30, bbyhigh=     1.0000e+30, bbzhigh=     1.0000e+30  #
 # rotx   =     0.0000    , roty   =     0.0000    , rotz   =     0.0000      #
 #                                                                            #
 ##############################################################################
 # doit, ?, return, help                                                      #
 ##############################################################################

showlines= [yes|no]:
Flags, whether the Materialplot shall have Lines where the Material Boundaries cross Gridplanes.
text= [yes|no]:
Flags, whether the Annotation-Text that has been specified via text()= bla bla in the Section -general should be plotted together with the Material Boundaries.
scale= SCALE:
The initial Zoom Factor of the resulting Plot.
plotopts= ANY STRING CONTAING OPTIONS FOR gd1.3dplot:
gd1 does not display the Data itself, but writes a Datafile for gd1.3dplot and starts gd1.3dplot to display these Data.
Useful Options are:
- -colorps : Produce colour PostScript and quit
- -greyps : Produce grey-scale PostScript and quit
- -geometry X11-GEOMETRY : Initial Geometry for the X11 Window of gd1.3dplot.
- -o FILENAME : If a PostScript is requested, the File written is FILENAME. The default Filename is dataplot.ps.
eyeposition= (XEYE, YEYE, ZEYE):
This specifies the initial Eyeposition for the 3D Plot that will be produced. As soon as the Plot appears, you can interactively change the Eyeposition with the Buttons of gd1.3dplot, but for a complex Geometry, this may take some Time.
bbxlow=,bbxhigh=,bbylow=bbyhigh=,bbzlow=,bbzhigh=:
Specifies the Coordinates of a Bounding Box. Only the Materialboundaries that lie within the Box are plotted. Use this if you want to see the Materialdistribution in a Plane.
rotx= PhiX, roty= PhiY, rotz= PhiZ:
This specifies the Parameters of an additional Rotation Matrix. The Data is rotated around the x-Axis by an angle of PhiX, then the Result is rotated around the y-Axis by an angle of PhiY, and finally the Result is rotated around the z-Axis by an angle of PhiZ.
doit:
If you say "doit", the relevant Settings in "-mesh" are checked, the Mesh is generated, and the Material-Boundaries are plotted.

Example The following shows the Material Distribution of a Waveguide Twist again, this Time, the Parameter bbyhigh is specified such, that only the Material Boundaries behind the Plane y=0 are shown.

 include(/usr/local/gd1/examples-from-the-manual/ggcylinder-twisted.gdf)
 -volumeplot
    eyeposition= ( 1, 2, 1.3 )
    scale= 4.5
 bbyhigh= 0
    doit

**Figure 1.29:** A twisted Waveguide. Only the Material Boundaries behind the Plane y=0 are shown.
$\begin{figure}\centerline{ \psfig{figure=volumeplot-bbzhigh-eq-ZZ.ps,width=18cm,bbllx=-2pt,bblly=-2pt,bburx=716pt,bbury=556pt,clip=} }\end{figure}$

Example The following shows the Material Distribution of a Waveguide Twist again, this time, the Parameter roty is specified nonzero.

 include(/usr/local/gd1/examples-from-the-manual/ggcylinder-twisted.gdf)
 -volumeplot
    eyeposition= ( 1, 2, 1.3 )
    scale= 4.5
 roty= 20
    doit

**Figure 1.30:** A twisted Waveguide. The Plot is rotated slightly around the y-Axis.
$\begin{figure}\centerline{ \psfig{figure=volumeplot-roty-eq-YY.ps,width=18cm,bbllx=-2pt,bblly=-2pt,bburx=716pt,bbury=556pt,clip=} }\end{figure}$

-cutplot: Shows the resulting Mesh in a selected Meshplane

This Section enables the Generation of the Grid and shows only in a selected gridplane the discretised Material Boundaries as generated from the geometric Primitives specified so far.

A similar Effect can be achieved with the Section -volumeplot with the Aid of the Parameters bb?low, bb?high.

 ##############################################################################
 # Flags: nomenu, noprompt, nomessage,                                        #
 ##############################################################################
 # Section: -cutplot                                                          #
 ##############################################################################
 # onlyplotfile= no                     -- don't display Plot                 #
 # draw  = both                         -- both | approximated | input        #
 # grid  = yes                          -- yes|no                             #
 # normal= z                            -- Plane Normal of the Cut-Plane      #
 # cutat = undefined                    -- The Coordinate of the Cut-Plane    #
 #                                                                            #
 # plotopts= -geometry 800x668+410+40 -noclip                                 #
 # eyeposition= ( -1.0, -2.30, 0.50 )                                         #
 ##############################################################################
 # doit, ?, return, help                                                      #
 ##############################################################################

draw= [both|approximated|input]:
Flags, whether the Materialboundaries should be plotted both as diagonal Mesh Fillings and as smooth Mesh Fillings (both), or only as diagonal Mesh Fillings (approximated), or only as smooth Mesh Fillings (input).
grid= [yes|no]:
Flags, whether the Positions of the Grid Planes shall be plotted together with the Material Approximation.
normal= [x|y|z], cutat= :
cutat: The Coordinate Value of the Gridplane in Direction normal where the Material Filling shall be plotted.
plotopts= ANY STRING CONTAINING OPTIONS FOR gd1.3dplot:
gd1 does not display the Data itself, but writes a Datafile for gd1.3dplot and starts gd1.3dplot to display these Data.
Useful Options are:
- -colorps : Produce colour PostScript and quit
- -greyps : Produce grey-scale PostScript and quit
- -geometry X11-GEOMETRY : Initial Geometry for the X11 Window of gd1.3dplot.
- -o FILENAME : If a PostScript is requested, the File written is FILENAME. The default Filename is dataplot.ps .
eyeposition= (XEYE, YEYE, ZEYE):
This specifies the initial Eyeposition for the 3D Plot that will be produced. As soon as the Plot appears, you can interactively change the Eyeposition with the Buttons of gd1.3dplot, but for a complex Geometry, this may take some Time.
doit:
If you say "doit", the relevant Settings in "-mesh" are checked, the Mesh is built, and the Material Boundaries in the selected Plane are plotted.

Solver sections: Eigenvalues and driven Time Domain Problems

-eigenvalues

 ##############################################################################
 # Flags: nomenu, noprompt, nomessage,                                        #
 ##############################################################################
 # section -eigenvalues                                                       #
 ##############################################################################
 # solutions    = 15                                                          #
 # estimation   = undefined                                                   #
 # storeallmodes= no                                                          #
 #    flowsave  = 0.0                                                         #
 #    fhighsave = 1.0e+30                                                     #
 # passes       =  2                                                          #
 # pfac2        = 1.0e-3                                                      #
 # lossy          = no                  -- Lossy or dispersive Computation    #
 #     flowsearch = undefined           -- Edges of the search Region...      #
 #     fhighsearch= undefined           -- ...when "lossy= yes"               #
 #   -ports                             -- ...when "lossy= yes"               #
 #   -linitialfields                    -- ...when "lossy= yes"               #
 #                                                                            #
 #                                                                            #
 # compressed   = no                    -- Minimal RAM, more CPU and IO Time  #
 ##############################################################################
 # return, doit, help, ?                                                      #
 ##############################################################################

solutions= NSOL:
The Number of Basis Vectors to use for solving the Eigenvalue Problem. This Number should better not be smaller than, say, 15. The more Basis Vectors you allow, the more accurate the Solutions will be. But: The Memory Requirement and roughly also the CPU Time is proportional to this Number. If compressed= yes is specified, the Memory Requirement is NOT proportional to the Number of Basisvectors, as then the Basisvectors are compressed and stored to Files and retrieved from Files. The compressed Basisvectors are written to Files with Names built from the scratchbase Parameter of Section -general.
estimation= FUP:
Estimation of the resonant Frequency of the highest Mode, i. e. the NSOL.st Mode.
This Parameter is mandatory.
A common Error, that even we run into, is, to specify this Estimation badly wrong. To get an Estimate, compute with a coarse Mesh, specify the estimated highest Frequency quite high, and compute. The Estimate is good, if gd1 finds about 20% good Modes less than you were asking for.
storeallmodes= [yes | no]:
Selects whether even the static Modes shall be saved.
gd1 computes normally 20 to 30 % static Modes (when passes=1), but does not store them. If you do not believe that these static Modes are really static, you can enforce the storing to File with this Option. When the static Solutions are in the outfile, you can view these 'Solutions' with gd1.pp.
flowsave= FLOW, fhighsave= FHIGH:
The Frequency Range, where resonant Fields shall be stored to Outfile. This is really only useful when computing in Parallel, and there is enough Diskspace on the Compute-Nodes to hold the intermediate Files, but not enough Diskspace on the Master-Node to hold all the Results of the Computation. For such Situations, you may also specify -general, dice= yes, iodice= yes, which specifies that the Resultfields shall be stored on the local Disks of the Compute Nodes. BUT: -general, dice= yes, iodice= yes can only be used for the PVM Version, not the MPI Version.
passes= NPASS:
gd1 uses an Algorithm of Tückmantel^1.4 ^1.5 to solve the Eigenproblem. This Algorithm establishes a Set of NSOL Basisvectors that are mutually Orthogonal and (hopefully) span only the Subspace also spanned by the Eigenvectors corresponding to the NSOL lowest Eigenvalues.
But since gd1 solves the Eigenproblem resulting from the discretised Version of
$[\varepsilon]^{-1} {\rm\nabla \times }[\mu]^{-1} {\rm\nabla \times }\vec{E} = \omega^2 \vec{E}$ , gd1 normally finds 20 to 30 % Eigenvalues very near to Zero. These Eigenvalues belong to static Fields, $\omega=0$ .
If you specify passes1, gd1 throws away the static Components in its already established Basis Vectors and can find more resonant Modes with the same specified NSOL. Also, the Accuracy of the Fields becomes somewhat better.
pfac2= PFAC2:
gd1 uses an Algorithm of Tückmantel to solve the algebraic Eigenproblem resulting from the discretised MAXWELLian Equations. This Algorithm has an internal accuracy Factor, called pfac2, that controls the relative Cleaning of the Basisvectors from Eigenvectors outside the Range 0 to FUP, in which the NSOL resonant Fields are expected.
A smaller pfac2 leads to increased CPU-Time, but better Accuracy for the lower Modes. A good Value is pfac2=1e-3.
lossy= [yes|no]:
When lossy= yes, Eigenvalues are searched in a Model where the lossy Parameters and dispersive Parameters of Materials with type= normal are taken into Account. This Algorithm needs four times as much Memory as the lossfree Algorithm.
flowsearch= F1, fhighsearch= F2:
Only used when lossy=yes: The Frequency Range where the Resonances of the lossy Device are searched in.
-ports:
When lossy= yes, absorbing Boundary Conditions are applied at Ports that are specified via -eigenvalues,-ports. The Section -eigenvalues,-ports is the same as the Section -fdtd,-ports.
-linitialfields:
When lossy= yes, Initial Fields can be loaded as starting Field.
The Section -eigenvalues,-linitialfields is the same as the Section -fdtd,-linitialfields.
compressed:
If compressed=yes, the Basis Vectors will be compressed and stored to Scratchfiles and re-read when needed. This takes much less Memory during the Eigenvalue computation, but increases substantially the Input-Output Time.
doit:
If you say "doit", the Settings in "-general, -mesh, -material" are checked, the Mesh is generated, and the Iteration for the resonant Fields is performed.
After the Field Computation, the Fields are written to File and the Program stops.

Example The following specifies that we want to compute with 15 Basisvectors, we want to perform two Passes to search for the Eigenvalues, and we estimate that the highest resonant Frequency of the 15 to be found will be about 1.3 GHz. The final doit starts the Eigenvalue Computation.

 -eigenvalues
   solutions= 15
   passes= 2
   estimation= 1.3e9
   doit

-fdtd: Compute time dependent Fields

This Section shows the Subsections that only make Sense for Time Domain Computations. The "doit" in this Section starts the Time Domain Computation.

 ##############################################################################
 # Flags: nomenu, noprompt, nomessage,                                        #
 ##############################################################################
 # Section: -fdtd                                                             #
 ##############################################################################
 # -ports                     -- Absorbing Boundary Conditions.               #
 # -pexcitation               -- Excited Port Modes.                          #
 # -lcharges                  -- One or more relativistic Line Charges.       #
 # -windowwake                -- Wakes in a moving Mesh Window.               #
 # -clouds          -- not yet finished.                                      #
 # -linitialfields            -- Loads initial Fields at t=0.                 #
 # -voltages                  -- Enforce Voltages between Points.             #
 # -decaytime                 -- z-dependent Damping.                         #
 # -time                      -- Timestep etc.                                #
 # -storefieldsat             -- When to store Fields.                        #
 # -fexport                   -- When to store Fields.                        #
 # -smonitor                  -- What Flux Quantities to store.               #
 # -fmonitor                  -- What Field Quantities to store.              #
 # -pmonitor                  -- What Power Quantities to store.              #
 #                                                                            #
 # hfdtd= no                  -- Use higher Order Curl-Operators.             #
 ##############################################################################
 # doit, ?, return, help                                                      #
 ##############################################################################

-ports:
Branches to the Sub-Section -fdtd/-ports where you specify the Location of "ports" and the Properties of these Ports.
-pexcitation:
Branches to the Sub-Section -fdtd/-pexcitation, where you specify the Center Frequency, the Bandwidth and the Amplitudes of selected Modes of selected Ports.
-lcharges:
Branches to the Sub-Section -fdtd/-lcharge, where you specify the Properties of relativistic Line Charges.
-windowwake:
Branches to the Sub-Section -fdtd/-windowwake, where you specify the Properties of a moving Mesh Window to compute the Wakepotential of relativistic Line Charges.
-clouds:
Branches to the Sub-Section -fdtd/-clouds, where you specify the Properties of non-relativistic Charge Clouds.
-linitialfields:
Branches to the Sub-Section -fdtd/-linitialfields, where you specify what Fields shall be the Initialfields of a Time dependent Computation.
-voltages:
Branches to the Sub-Section -fdtd/-voltages, where you specify excited Voltages between arbitrary Points.
-decaytime:
Allows z-dependent Damping of the Fields without specifying a graded lossy Dielectric.
-time:
Branches to the Sub-Section -fdtd/-time, where you specify the minimum and maximum allowed Simulation Time.
You can also specify the Times where the electric and magnetic Fields are written.
-storefieldsat:
Branches to the Sub-Section -fdtd/-storefieldsat. You can specify multiple Time-Ranges where the electric and/ or magnetic Fields are stored to Files.
-fexport:
Allows Writing of selected Field Parts as ASCII Files during the Time Domain Computation. This is useful for making Movies.
-smonitor:
Branches to the Sub-Section -fdtd/-smonitor, where you specify what Scalar Quantities shall be monitored during the Time Domain Computation.
-fmonitor:
Branches to the Sub-Section -fdtd/-fmonitor, where you specify what Field Quantities shall be monitored during the Time Domain Computation.
-pmonitor:
Branches to the Sub-Section -fdtd/-pmonitor, where you specify what Power Quantities shall be monitored during the Time Domain Computation.
doit:
If you say "doit", the Settings in "-general, -mesh, -material" are checked, the Mesh is generated, and the Iteration for the Time dependent Fields is performed.
While the Field Computation is running, the Amplitudes of selected Port Modes are written, and selected electric and magnetic Fields are written. Also selected scalar, Field or Power Quantities are written. If a Wake Computation is performed, the Data required for the Computation of Wakepotentials is also written. These Amplitudes and Fields (and Wake-Data) can be processed further by gd1.pp. It is not needed to wait until the Time Domain Computation has finished. gd1.pp mat be used while the Computation is running, to analyse the Data which is already available. After the Field Computation, the Program stops.

-fdtd,-ports/ -eigenvalues,-ports

The Section -time,-ports is the same as -eigenvalues,-ports.

A "Port" is a Part of the Border of the computational Volume that shall be treated as an infinitely long Waveguide. In this Section you specify the Location of Ports. You also specify the Number of Modes whose time Amplitudes shall be written to File.

 ##############################################################################
 # Flags: nomenu, noprompt, nomessage,                                        #
 ##############################################################################
 # Section: -ports                                                            #
 ##############################################################################
 # name  = noname-001                                                         #
 # plane = xlow                                                               #
 # modes = 1                                                                  #
 #(pxlow=      -1.0e+30    , pxhigh=       1.0e+30    ) Ignored for plane=xlow
 # pylow=      -1.0e+30    , pyhigh=       1.0e+30                            #
 # pzlow=      -1.0e+30    , pzhigh=       1.0e+30                            #
 # epsmaximum= 2.0                                                            #
 # muemaximum= 1.0                                                            #
 # npml      = 40                  -- No of PML-Planes                        #
 # dampn     = 50.0e-3             -- Damping factor in last Plane            #
 # enforcemesh= yes                -- Enforce translational invariant Mesh    #
 ##############################################################################
 # doit, list, ?, return, help                                                #
 ##############################################################################

name = ANY-STRING-WHICH-COULD-SERVE-AS-FILENAME:
Specifies the Name of the Port.
This Name is used, eg. to identify the Port later on. If you enter the Name of an already defined Port, you will edit the Parameters for this already defined Port.
The Length of the name has to be less or equal 64 Characters.
plane= [xlow|xhigh|ylow|yhigh|zlow|zhigh]:
Specifies at which of the six limiting Planes of the computational Volume the Port is located on.
modes= NMODES:
Number of orthogonal Modes whose Amplitudes shall be monitored. This Number may be zero. The absorbing Boundary Conditions work independently of the orthogonal Modes, so there is no need to specify a large Number here.
No port Amplitudes are monitored when performing a lossy Eigenvalue computation.
pxlow, pxhigh, pylow, pyhigh, pzlow, pzhigh:
Specifies the Rectangle where the Port is in. These Parameters are needed if there is more than one Port at one of the six possible Planes [x|y|z][low|high].
If the Port is at xlow or at xhigh, the Values for pxlow and pxhigh are ignored. If the Port is at ylow or at yhigh, the Values for pylow and pyhigh are ignored. If the Port is at zlow or at zhigh, the Values for pzlow and pzhigh are ignored.
epsmaximum, muemaximum:
Values of the "densiest" Materials at the port. These Values are used to compute the Patterns of the Port-Modes.
npml:
The Number of "Perfectly Matched Layers" to use as absorbing Boundary Conditions.
30 is a good Value.
If a relativistic Charge enters or exits the computational Volume through the Port, you should choose a Value of 40 or more.
dampn:
The damping Factor of the outermost "Perfectly Matched Layer".
doit:
Stores the current Data and enables the editing of the Parameters of a Port that is not yet defined (a new Port).
list:
Lists the Names of the already defined Ports.

Example The following specifies that we want to have attached four Ports: Two are at the lower x-Boundary, the Names are xlow1, xlow2. Two Ports are at the upper x-Boundary of the computational Volume, the Names are xhigh1, xhigh2. The Ports at the same Boundary are distinguished by their pzlow, pzhigh Parameters.

-fdtd
  -ports
     name= xlow1,  plane= xlow , pzlow= 0,  modes= 10, doit
     name= xhigh1, plane= xhigh, pzlow= 0,  modes= 2, doit
     name= xlow2,  plane= xlow , pzhigh= 0, modes= 2, doit
     name= xhigh2, plane= xhigh, pzhigh= 0, modes= 2, doit

-fdtd,-pexcitation: What Port-Mode shall be excited

Here you may specify what Port-Excitation shall be used. The Excitation can be a switched on Sine-signal, a Gaussian Pulse modulated with a Sine, or a user specified Signal.

 ##############################################################################
 # Flags: nomenu, noprompt, nomessage,                                        #
 ##############################################################################
 # Section: -pexcitation                                                      #
 ##############################################################################
 # port  =  undefined                                                         #
 # mode  = 1                                                                  #
 # amplitude = 1.0                                                            #
 # phase     = 0.0                                                            #
 # frequency = undefined                                                      #
 # bandwidth = undefined                                                      #
 # risetime  = 0.0                                                            #
 # signalcommand= -none-                                                      #
 ##############################################################################
 # nextport, list, ?, return, help                                            #
 ##############################################################################

port= NAME-OF-AN-ALREADY-DEFINED-PORT:
The Name of the Port where the Mode shall be launched. This is a Name that you have used in the Section "-fdtd/-ports".
mode:
The Number of the Mode to launch. The Modes are numbered sequentially, starting from 1. The Modes are sorted by the negative real Part of the Square of their propagation Constants.
amplitude:
The Amplitude of the Mode to launch. If the Amplitude is Zero, no Mode is launched. If you specify a monochromatic Excitation, i.e. if you specify a "risetime" $\ne$ 0, then the Power of the excited Wave in the steady state is "amplitude" Watts. If you specify a broadband Excitation, then the maximum Power of the excited Wave is approximately "amplitude" Watts.
phase:
The Phase of the Excitation. This is probably only useful when more than one Mode is excited.
frequency:
If "risetime $\ne$ 0", i.e. when using a monochromatic Excitation, the Frequency of the Excitiation. When "risetime = 0", i.e. when using a broadband Excitation, the Centerfrequency of the Excitation.
bandwidth:
The Frequency Bandwidth of the time Signal to use as Excitation.
risetime:
If specified as Nonzero, a monochromatic Excitation is used. The Risetime of the Excitation is "risetime".
list:
Lists the Names and Planes of the Ports as specified in Section "-fdtd/-ports".
signalcommand= NAME_OF_COMMAND:
If specified as -none-, the Excitation will be computed from risetime, frequency, bandwidth and amplitude. If specified as any other String, every XXX Timesteps the specified Command is executed to compute the Signal at the next XXX Timesteps. The Command is executed as:
```
       NAME_OF_COMMAND < ./gdfidl-actual-time-interval > ./gdfidl-actual-signal
```
The File ./gdfidl-actual-time-interval contains the following Data:
- In the first Line there are iTime1, iTime2, TimeStep
  - iTime1: The Number of the first Timestep for which the Signal shall be defined.
  - iTime2: The Number of the last Timestep for which the Signal shall be defined.
  - TimeStep: The Width of a Timestep.
- in the second Line there are Beta, Alpha, DeltaZ.
  - Beta: The real Part of the propagation Constant of the selected Mode at the selected Frequency frequency.
  - Alpha: The imaginary Part of the propagation Constant.
  - DeltaZ: The Width of the Mesh at the selected Port.
The Signalcommand NAME_OF_COMMAND has to write to stdout simply the Values of the Signal at the Timesteps iTime1 to iTime2, one line for each value.
nextport:
Switches to the next Port-Excitation. For the next Ports, you may specify different Parameters port, mode, amplitude and phase, but the Parameters frequency, bandwidth and risetime are the same for all excited Ports.

Example The following specifies that the fundamental Mode of the Port with Name InputPort shall be excited. Its Amplitude shall be '1', the Centerfrequency of the excited Pulse shall be 1.2 GHz, and the Bandwidth of the excited Pulse shall be 0.7 GHz.

 -fdtd,
    -pexcitation
        port= InputPort
        mode= 1
        amplitude= 1
        frequency= 1.2e+9
        bandwidth= 0.7e+9

Example The following specifies that the fundamental Mode of the Port with Name InputPort1 shall be excited. Its Amplitude shall be '1', the Frequency of the excited Signal shall be 1.2 GHz, and the Risetime until Steady State of the Excitation shall be 10 HF-Periods. In Addition, the fundamental Mode of the Port with Name InputPort2 shall be excited. Its Amplitude shall be '1'.

 -fdtd,
    -pexcitation
        port= InputPort1, mode= 1, amplitude= 1, phase= 0
        frequency= 1.2e9, risetime= 10 / 1.2e9
      nextport
        port= InputPort2, mode= 1, amplitude= 1, phase= 0

Example The following specifies that the fundamental Mode of the Port with Name InputPort shall be excited. The Portmodes Pattern shall be computed for a Frequency of 10 GHz, and the Signal of the Excitation shall be defined by an external Signal-command.

 -fdtd,
    -pexcitation
        port= InputPort
        mode= 1
        amplitude= 1
        frequency= 10e9
 #
 # Compile the Signalcommand.
 #
 system($F90 signal-command.f -o signal-command)
        signalcommand= ./signal-command

This is the Sourcefile signal-command.f:

      PROGRAM SignalCommand
      IMPLICIT DOUBLE PRECISION (a-h,o-z)

      Pi= 4*ATAN(1.0d0)
      Frequency= 10e9
      TRise= 10/Frequency
      TDecay= 20/Frequency
      THold= 50/Frequency
      READ (*,*) iTime1, iTime2, TimeStep
      READ (*,*) Beta, Alpha, DeltaZ
      DO iTime= iTime1, iTime2, 1
         ActualTime= iTime*TimeStep
         IF (ActualTime .LE. TRise) THEN
            Phi= ActualTime * Pi / TRise
            Factor= (1-COS(Phi))/2
         ELSE IF (ActualTime .LE. TRise+THold) THEN
            Factor= 1
         ELSE IF (ActualTime .LE. TRise+THold+TDecay) THEN
            Phi= (ActualTime - (TRise+THold)) * Pi / TDecay
            Factor= (1+COS(Phi))/2
         ELSE
            Factor= 0
         ENDIF
         Factor= Factor * TimeStep / DeltaZ
         WRITE (*,*) Factor*SIN(2*Pi*Frequency*ActualTime)
      ENDDO
      END PROGRAM SignalCommand

-fdtd,-lcharge: Properties of relativistic Line-Charges

In this Section one specifies the Properties of one or several relativistic Line-Charges. When computing with the conventional Scheme, i.e. not with the Windowwake Algorithm, one can specify up to 100 Linecharges, each with a different Charge, different Position, different Distribution and different Direction of Flight. When using the Windowwake Algorithm, all Charges must go in positive z-Direction, and they must have the same Shape. They may differ in their Positions and Charge. Once the Properties of a Linecharge are specified, one switches to the next Linecharge with the Command 'nextcharge'.

The standard Usage of this Section is to compute Wakepotentials. When a nonzero Charge is specified, and a Time Domain Computation is performed, the Wakepotentials are computed as the Potential that is seen by Witness Particles that are traveling in positive z-Direction. When the conventional Scheme is used, Fields and Port Amplitudes may be stored and monitored as well.

 ##############################################################################
 # Flags: nomenu, noprompt, nomessage,                                        #
 ##############################################################################
 # Section: -lcharge                                                          #
 ##############################################################################
 # ----- Parameters of a Line Charge: ------                                  #
 # charge    =        0.0               -- [As]                               #
 # shape     = gaussian                 -- gaussian | triangular | table      #
 #    tablefile=  -none-
 #    xtable =        1.0               -- [m]                                #
 # sigma     =  undefined               -- [m]                                #
 # isigma    =  6                       -- Number of Sigmas to use.           #
 # xposition =        0.0               -- [m]                                #
 # yposition =        0.0               -- [m]                                #
 # direction = +z                       -- +z, -z                             #
 # soffset   =        0.0               -- [m]                                #
 # beta  =        1.0                   -- [1], quite a Hack, if not 1.       #
 # ----- Other Parameters: ------                                             #
 # shigh     =       auto               -- [m]                                #
 # showdata  = no                       -- ( yes | no )                       #
 # napoly    = yes                      -- ( yes | no )                       #
 #   naccuracy=      10.0e-6     -- wanted acc for poisson-eq in Napoly alg.  #
 #   ignoretem= yes                     -- should be "yes" for Wx, Wy         #
 ##############################################################################
 # ?, nextcharge, return, help                                                #
 ##############################################################################

charge:
The total Charge of the Linecharge.
If the Position of the Charge is specified such that the Charge travels along a magnetic Plane, the Charge taken for the computational Volume is half the Value.
If the Charge travels along two Planes of Symmetry simultaneously, the Charge in the Volume is a Quarter of the specified Charge.
This Way, the excited Wakefields in a Half or a Quarter of the Structure are the same as if the Charge has traveled in a full Structure.
shape:
The Shape of the Linecharge. Possible Values are gaussian, triangular and table.
tablefile:
The Filename of a Shape-Table. If a Tablefile is given, that Data is taken to describe the Charges Shape. The total Charge as described in the Table is ignored, only the Shape as described in the Table is used. The Parameter sigma is then ignored.
xtable:
Scale Factor to apply to the Position Values in the Table.
sigma:
The Width of the Gaussian Linecharge or the Width of the Triangle.
isigma:
This Parameter is used to control how long the Gaussian Linecharge shall be considered Nonzero. For a Computation with -windowwake it might be useful to specify isigma=3. Then, the Length of the computational Window extends from -3*isigma before the Center of the Charge up to shigh behind the Center of the Charge.
xposition, yposition:
The Position of the Linecharge in the x-y-Plane.
direction:
The Direction of Flight of the Linecharge. The standard Value is '+z' and that is the Value to use for computing Wakepotentials.
soffset:
The s-Offset of the Linecharge. Given in Metres. A larger Value for soffset has the Effect that the Charge travels later through a given z-Plane.
shigh:
The s-Coordinate of the last Wakepotential wanted. Possible Values are "auto" or a positive Real. If "shigh= auto", a Value of "20 * sigma" is taken.
showdata= [yes|no]:
If "yes", some diagnostic Plots concerning the Wakepotential are shown when the Time Domain Computation starts.
napoly= [yes|no]:
If napoly= yes, near the z-Borders of the computational Volume, an Integration of the Wakefield similiar to the Napoly-Integration is performed. This Option should be set to napoly= yes for scraper-like structures. One can keep the Option set even if it is no needed, as GdfidL checks whether such an Integration is useful. If it is not, it is not done.
ignoretem= [yes|no]:
Should be "yes" for Wx, Wy. When ignoretem=yes, the Term proportional to the primary Field of the exciting Charge is ignored.
nextcharge:
Stores the current Data and enables Editing of the Parameters of the next Linecharge.

Example The following specifies that we want to model a Linecharge travelling with the Speed of Light along the Axis (x,y)=(0,0). The total Charge of the Linecharge shall be 1 pC, and its Gaussian Width sigma shall be 1 mm. We are interested in s-Values up to 100 mm.

 -lcharge
    xpos= 0
    ypos= 0
    charge= 1e-12
    sigma= 1e-3

    shigh= 100e-3

Example An Example for a Table File describing a Charges Shape is given below.

# -lcharge
#    shape= table, tablefile= Bunch1.txt
#    xtable= 1e-6, charge= 1e-12
#
# Everything behind a '#' is ignored.
# Lines in the Tablefile may be empty, or they may
# contain two (or more) Numbers.
# The first Number is a Position, the next Number is
# a relative Charge. What follows behind these two Numbers is ignored.
#
# bunch1 (linac entrance)
# s[microns]   Charge
# ________________________________________________


0,      0
1       -1.32067
2       -1.10711
3       -0.894051
4       -0.6815
5       -0.469454
6       -0.25791
7       -0.046869
8       0.16367
9       0.373709
10       0.583247

Example An Example how to specify four Line-Charges that excite mostly quadrupole-Wakepotentials:

 define(CHARGE, 1e-12) define(SIGMA, 1e-3)
 define(RADIUS, SomeValue)

 define(RADIUSoSQRT2, RADIUS * (2**0.5) ) # Radius * Cos( 45 Degrees )
 -lcharge
         xposition=  RADIUSoSQRT2, yposition=  RADIUSoSQRT2
         charge= CHARGE, sigma= SIGMA, soffset= 0
      nextcharge
         xposition= -RADIUSoSQRT2, yposition=  RADIUSoSQRT2
         charge= -CHARGE, sigma= SIGMA, soffset= 0
      nextcharge
         xposition= -RADIUSoSQRT2, yposition= -RADIUSoSQRT2
         charge=  CHARGE, sigma= SIGMA, soffset= 0
      nextcharge
         xposition=  RADIUSoSQRT2, yposition= -RADIUSoSQRT2
         charge= -CHARGE, sigma= SIGMA, soffset= 0

Example

 # /usr/local/gd1/examples-from-the-manual/quadrupole.gdf
 #
 # This Device has two Planes of Symmetry.
 # These Planes of Symmetry are NOT used here.
 # Four Charges are specified such that
 # the excited Wakefields are mainly quadrupole Wakefields.

 -general,
     outfile= /tmp/UserName/bla
     scratch= /tmp/UserName/scratch

 define( A , 2*0.038 )
 define( A2, 2*0.016 ) # x-Width

 define( B , 2*0.010 ) # y-Width
 define( B2, 2*0.002 )

 define(RANGE, 0.01)

 define(STPSZE, B/100 )
 -mesh
     spacing= STPSZE
     pxlow= -(A/2+STPSZE), pxhigh= (A/2+STPSZE), cxlow= ele, cxhigh= ele
     pylow= -(B/2+STPSZE), pyhigh= (B/2+STPSZE), cylow= ele, cyhigh= ele
     pzlow= -0.02, pzhigh= 0.02

 ##########
 -material, material= 3, type= electric

 # Fill the Universe with Metal:
 -brick
     material= 3
         xlow= -INF, xhigh= INF
         ylow= -INF, yhigh= INF
         zlow= -INF, zhigh= INF
     doit

 do ii= 1, 2

    # The Device also has a Plane of Symmetry at z=0.
    # Half of the Device is modeled here, and that Half
    # is rotated and translated to the wanted Position
    # and Orientation.

    -transform, reset
    if (ii == 1) then
       -translate, offset= ( 0, 0, -(0.01+RANGE+0.005/2) ), doit
    else
       -rotate, axis= ( 0, 1, 0 ), angle= 180, doit
       -translate, offset= ( 0, 0,  0.01+RANGE+0.005/2 ), doit
    end if

    -ggcylinder
        material= 0
        xprime= ( 1, 0, 0 )
        yprime= ( 0, 1, 0 )
        xslope= 0, yslope= 0  # Re-Set to the Default Values
        xscale= 1, yscale= 1  # Re-Set to the Default Values

        clear
           point= (  0   , -B /2 )
           point= (  A2/2, -B /2 )
           point= (  A /2, -B2/2 )
           point= (  A /2,  B2/2 )
           point= (  A2/2,  B /2 )
           point= ( -A2/2,  B /2 )
           point= ( -A /2,  B2/2 )
           point= ( -A /2, -B2/2 )
           point= ( -A2/2, -B /2 )
     show= later

         origin= ( 0, 0, 0 )
         range= ( 0, 0.01 )
         doit   # The wide and straight Part.

 # Same Cross-section, linear slopes:
         xslope= (0.033/0.038-1)/RANGE
         yslope= (0.011/0.012-1)/RANGE
         origin= ( 0, 0, 0.01 )
         range= ( 0, RANGE )
    show= later
         doit  # The tapered Part.

 # Same Cross-section, scaled
         xslope= 0, yslope= 0
         xscale= 0.033/0.038, yscale= 0.011/0.012
         origin= ( 0, 0, 0.01+RANGE )
         range= ( 0, 0.005 )
    if (ii == 1) then
       show= later
    else
       show= all
    end if
         doit  # The narrow and straight Part.
 end do

 -volumeplot, doit
 -mesh, perfectmesh= no
 ##########
 -ports
      name= Lower, plane= zlow, modes= 0, doit
      name= Upper, plane= zhigh, modes= 0, doit
 ##########
 define(CHARGE, 1e-12) define(SIGMA, 1e-3)
 define(RADIUS, B/10)
 define(RADIUSoSQRT2, RADIUS * (2**0.5) ) # Radius * Cos( 45 Degrees )
 -lcharge
         xposition=  RADIUSoSQRT2, yposition=  RADIUSoSQRT2
         charge= CHARGE, sigma= SIGMA, soffset= 0
      nextcharge
         xposition= -RADIUSoSQRT2, yposition=  RADIUSoSQRT2
         charge= -CHARGE, sigma= SIGMA, soffset= 0
      nextcharge
         xposition= -RADIUSoSQRT2, yposition= -RADIUSoSQRT2
         charge=  CHARGE, sigma= SIGMA, soffset= 0
      nextcharge
         xposition=  RADIUSoSQRT2, yposition= -RADIUSoSQRT2
         charge= -CHARGE, sigma= SIGMA, soffset= 0

    shigh= 10 * SIGMA

 -fdtd, doit

**Figure 1.31:** A Device with three Planes of Symmetry. The Planes of Symmetry at x=0 and y= 0 could be used with a Computation with Linecharges. This is not used here. Four Charges are specified such that mainly quadrupole-Wakefields are excited.
$\begin{figure}\begin{center}% \quad \quad \psfig{figure=Quadrupole.ps,width=18cm,bbllx=202pt,bblly=174pt,bburx=503pt,bbury=372pt,clip=} \end{center} \end{figure}$

**Figure 1.32:** The Wakepotential as a Function of (x,y) near s=0. The Input for gd1.pp was: -gen, inf @last, -wakes, watsi= 0, doit
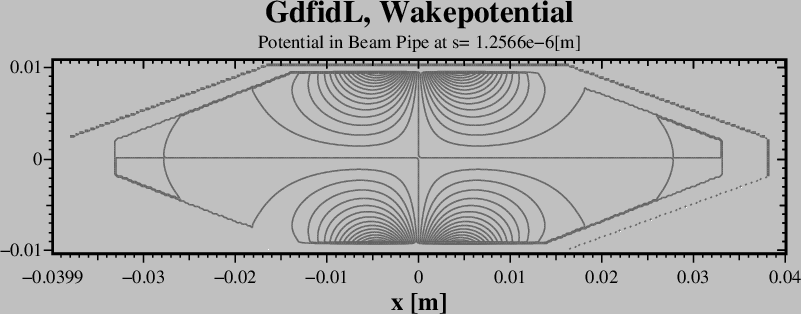$\begin{figure}\begin{center}\quad \quad \psfig{figure=QuadrupoleWat0.ps,width=18cm,bbllx=60pt,bblly=160pt,bburx=718pt,bbury=422pt,clip=} \end{center} \end{figure}$

-fdtd,-windowwake: Wakepotential in a moving computational Window

Here you specify the Properties of a computational Window which flies with the Velocity of Light synchronously with the exciting Charges.

 ##############################################################################
 # Flags: nomenu, noprompt, nomessage,                                        #
 ##############################################################################
 # Section: -windowwake                                                       #
 ##############################################################################
 # strangsplitting= yes                                                       #
 # fdtdorder= 31              -- What Order of FDTD Algorithm to take [1,31]  #
 # periodic  = no             -- Assume periodic Device.                      #
 #    nperiods=   100         -- Maximum Number of Periods to consider.       #
 #    modstore=    10         -- Store Wakepotentials after simulating        #
 #                            --   Multiples of modstore*(pzhigh-pzlow).      #
 ##############################################################################
 # doit, ?, return, help                                                      #
 ##############################################################################

strangsplitting:
Possible Values are "yes, no".
If strangsplitting=yes, a Scheme with splitted Updates for the z-transverse Components and z-longitudinal Components is used. This Scheme has negligible Dispersion Error for TEM-waves propagating in z-Direction. The Dispersion Error for other Kind of Waves is comparable to a first order FDTD Scheme.
fdtdorder:
Possible Values are [1,31].
If strangsplitting=no, and fdtdorder=1, the normal FDTD Algorithm is used to advance the electromagnetic Fields. If strangsplitting=no, and fdtdorder=31, a modified FDTD Algorithm is used to advance the electromagnetic Fields. That Scheme has zero Dispersion for Waves going in x- or y- or z-Direction and less Dispersion-Error than strang-Splitting for all Kind of Waves.
periodic:
Possible Values are "yes, no".
If periodic= no, the Length of the Geometry as specified via
-mesh, pzlow= ZLOW, pzhigh= ZHIGH is used for computing the Wakepotential.
If periodic= yes, the Length of the Geometry as specified via
-mesh, pzlow= ZLOW, pzhigh= ZHIGH is assumed to be one Period of a finite periodic Structure with Number of Periods given by nperiods= NP. After computing the Fields in a Multiple of modstore= MP periods, the Wakepotentials so far are recorded to the Database.
nperiods= NP:
Number of Periods to compute when periodic=yes.
modstore= MP:
At which Periods to store the intermediate Results.

Note: The Parameters of the exciting Linecharge are taken from the section -lcharge. The moving computational Window has a Length of isigma*sigma + shigh. The used Grid-Spacing in z is the Minimum of all the x-Spacings and y-Spacings and, if the specified "zspacing" in Section "-mesh" is smaller, then that zspacing is used.

Napoly-like Integration is performed, and cannot be switched off.

The Memory Requirement is proportional to the Length of the moving computational Window, i.e. proportional to isigma*sigma + shigh. One should not specify a large Value for shigh, in particular not longer than the structure Length, otherwise a conventional Wakepotential Computation is more economic.

The CPU Requirement is proportional to the Length of the moving Window times the Length over which the moving Window must travel. That Length is the z-Extension of the Structure plus the Length of the Window. The CPU Requirement is proportional to (isigma*sigma + shigh) * (pzhigh-pzlow + isigma*sigma + shigh). Any specified Port is ignored. The x- and y-Extension of the computational Volume must be specified large enough that Reflections from the x- and y-Borders cannot change the Wakepotentials. E.g. Waveguides going in x- or y-Direction should be modeled with a Length of "shigh".

The Losses of Materials with type=impedance and of Materials with type=coating are taken into Account.

The Losses of dielectric Materials are ignored.

Only Fields specified via fexport will be exported.

The only other Result is the Wakepotential.

Example The following specifies that we want to compute the Wakepotential of a Linecharge travelling with the Speed of Light along the axis (x,y)=(0,0). The total charge of the Linecharge shall be 1 pC, and its Gaussian Width Sigma shall be 1 mm. We are interested in s-Values up to 20 mm.

 -lcharge
    xpos= 0, ypos= 0
    charge= 1e-12
    sigma= 1e-3
    shigh= 20e-3
 -windowwake
    doit

-fdtd,-clouds: Properties of nonrelativistic Clouds of Charge

This Section enables the computation with nonrelativistic Cloud Charges. As of today (October 2004) this PIC Computation is not yet fully finished. Since the planned Computations are not yet fully implemented, we do not even document the Usage of what is available. What is available is the Ejection of Clouds of Charge, the Computation of the induced electromagnetic Fields of these Charges, and the integration of the Lorentz-Forces on these Clouds.

If a 'Particle in Cell' Computation is badly needed, contact Warner Bruns Field Computations. It might be that by the Date that you read this, what you need is already available.

 ##############################################################################
 # Flags: nomenu, noprompt, nomessage,                                        #
 ##############################################################################
 # Section: -clouds                                                           #
 ##############################################################################
 # box        = no                                                            #
 #   fraction = 0.990                                                         #
 #   bverbose = no                                                            #
 # ejectioncommand= -none-                                                    #
 # ejectionsubroutine= -none-                                                 #
 #                                                                            #
 #                                                                            #
 ##############################################################################
 # ?, return, help                                                            #
 ##############################################################################

-fdtd,-linitialfields/ -eigenvalues,-linitialfields: Specifies the initial Fields

This Section enables the loading of initial Fields for a Time Domain Computation or a lossy Eigenvalue Computation. If no initial Fields are specified, the initial Fields will be assumed to be Zero for Time Domain Fields and random Fields for Eigenvalue Computations.

The initial Field is the Sum of the specified Fields.

 ##############################################################################
 # Flags: nomenu, noprompt, nomessage,                                        #
 ##############################################################################
 # Section: -linitialfields                                                   #
 ##############################################################################
 # infile   = ./previous_outfile                                              #
 #    symbol   = e_1                                                          #
 #    quantity = e                                                            #
 #    solution = 1                                                            #
 #    factor   = 1.0                                                          #
 #    torealpart= yes                                                         #
 #    static   = no                                                           #
 #    brz      = no                                                           #
 #      xmirror= none                                                         #
 #      ymirror= none                                                         #
 # abstatic = 0.0                                                             #
 # nbstatic = ( 0.0, 0.0, 1.0 )                                               #
 ##############################################################################
 # doit, ?, return, end, help                                                 #
 ##############################################################################

infile= NAME_OF_A_PREVIOUSLY_USED_OUTFILE:
The Name of an "outfile" of a previous Computation. The Grid of that previous Computation must be compatible with the Grid of the current Computation. The easiest Way to achieve this, is to load the Geometry for the current Computation from the same infile via the Section -lgeometry.
symbol= QUAN_ISOL:
This is the full Name of the Symbol to be processed.
quantity= QUAN:
This is the first Part of the "symbol".
solution= ISOL:
This is the last Part of the "symbol", the Index of the "symbol".
factor:
The Factor by which the specified Field shall be multiplied, before it is added to the specified Fields so far.
torealpart:
When performing a lossy Eigenvalue Computation, the Field can be put to the real Part or the imaginary Part of the Start-Vector. This Parameter is ignored for Time Domain Computations.
static:
If static= yes, the loaded Field will only be used to accelerate or deflect free moving Charges in the PIC-algorithm. If static= no, the loaded Field will be used as Part of the initial Condition for the electromagnetic Field.
brz:
Special Flag for loading a rotational symmetric magnetostatic Field. Ignore it. Only for PIC-Computations.
abstatic:
Only for PIC Computations: Amplitude of a uniform static magnetic Field.
nbstatic:
Only for PIC Computations: Direction of a uniform static magnetic Field.
doit:
The Properties of the specified Field are recorded in an internal Database. When the Time Domain or lossy Eigenvalue Computation starts, the Sum of all specified Fields will be used as initial Field.

Example The following specifies that we want to use the Grid of a previous Computation, that we want to load the electric Field of the first Mode of that same previous Computation with a Factor of '1'. In Addition, we want to load the magnetic Field of the same Mode with an Amplitude of '-1'. If the two Fields come from a resonant Field Computation, this has the Effect of loading the Mode with a Phase of -45 Degrees.

 #
 # As the Filename in two Places better be the same,
 # We define the Files Name as a Variable.
 #
 sdefine( INFILE, /tmp/UserName/resonant-computation )
  -lgeometry
     infile= INFILE
  -linitialfields
     infile= INFILE
     symbol= e_1, factor=  1, doit
     symbol= h_1, factor= -1, doit

-fdtd,-voltages: Voltage Sources between selected Points

During a Time Domain Computation (with a static Mesh, i.e. not windowwake), Voltages along Paths can be specified and measured. The recorded Data can by analysed by gd1.pp's -voltages section.

 ##############################################################################
 # Flags: nomenu, noprompt, nomessage,                                        #
 ##############################################################################
 # Section: -voltages                                                         #
 ##############################################################################
 # startpoint  = ( 0.0, 0.0, 0.0 )                                            #
 # endpoint    = ( 0.0, 0.0, 0.0 )                                            #
 # resistance  = 0.10                   -- [Ohm]                              #
 # inductance  = 0.0                    -- [Henry]                            #
 # amplitude   = undefined              -- [V]                                #
 # phase       = 0.0                    -- [Degs]                             #
 # frequency   = undefined              -- [1/s]                              #
 # bandwidth   = undefined              -- [1/s]                              #
 # risetime    = undefined              -- [s]                                #
 # logcurrent  = yes                                                          #
 # name        = noname-001                                                   #
 ##############################################################################
 # doit, ?, list, return, help                                                #
 ##############################################################################

startpoint, endpoint:
Startpoint and Endpoint of the Path. The Voltage is applied between these two Points.
resistance:
Inner Resistance of the Voltage Source.
inductance:
Inner Inductance of the Voltage Source.
amplitude, phase, frequency, bandwidth:
The Amplitude, Phase, Centerfrequency and Bandwidth of the Voltage Source.
risetime:
If specified Nonzero, the Voltage Source is switched on. Between Zero and risetime, the Voltage is switched on according to the Formula:

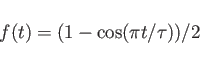$\begin{displaymath} f(t)= (1-\cos(\pi t/\tau))/2 \end{displaymath}$ (1.6)
logcurrent:
Whether the Current through the Voltage Source shall be monitored.
name:
The name of the Voltage Source.
doit:
The Data of the current Voltage Source is stored and the next Voltage Source can be specified.

If Voltage Sources are specified, the electric Field Strength between the Startpoint and Endpoint is measured while the Time Domain Computation is running. The Difference between the specified Voltage and the so measured Voltage is multplied by the Resistance of the Voltage Source. That Value is used as Current which is enforced to flow between the starting Point and Endpoint. The Current is low pass filtered with a time Constant given by $\tau=R/L$ .

The Values of the wanted Voltage, the measured Voltage and the Current can be inspected in the Postprocessor.

No Example yet.

-fdtd,-decaytime: Z-dependent damping Factor

During a Time Domain Computation (with a static Mesh, i.e. not windowwake), the Fields can be damped with a z-dependent damping Factor.

 ##############################################################################
 # Flags: nomenu, noprompt, nomessage,                                        #
 ##############################################################################
 # section -decaytime                                                         #
 ##############################################################################
 ## syntax:                                                                   #
 #  point= (Z_i, Tau_i)                                                       #
 ##############################################################################
 # clear, show, doit, ?, return, help                                         #
 ##############################################################################

point:
Specifies the next Point of the polygonal Description of the z-Dependency of the Decaytime.
clear:
Clears the polygonal Description.
show:
Gives a Plot of the polygonal Description.

Example

 -fdtd
    define(FREQ, 12e9)
    -decaytime
       clear
       point= ( -INF, 6000 / (@pi*FREQ) )
       point= ( Zmin, 6880 / (@pi*FREQ) )
       point= ( Zmax, 6580 / (@pi*FREQ) )
       point= (  INF, 6000 / (@pi*FREQ) )
      # show
       doit

-fdtd,-time: minimum / maximum Time, when to Store

In this Section one specifies the Time Parameters of a Time Domain Computation. Up to what Time to simulate, when to stop etc.

 ##############################################################################
 # Flags: nomenu, noprompt, nomessage,                                        #
 ##############################################################################
 # section -time                                                              #
 ##############################################################################
 # firstsaved    = undefined                                                  #
 # lastsaved     = undefined                                                  #
 # distancesaved = undefined                                                  #
 # tminimum      = undefined                                                  #
 # tmaximum      = undefined                                                  #
 # decaytime =       1.0e+30                                                  #
 ##############################################################################
 # amptresh =       3.0e-3                                                    #
 # dtsafety =       0.90                                                      #
 # ndt      = auto                                                            #
 # ___stopafter=       1.0e+30          -- Force Stop after that Time.        #
 # ___evmax    = undefined              -- Dangerous.                         #
 # ___dt       = undefined              -- Dangerous.                         #
 ##############################################################################
 # return, help, ?                                                            #
 ##############################################################################

firstsaved:
The first Time where the electric and magnetic Fields shall be stored to Files.
lastsaved:
The last Time where the Fields shall be stored to Files.
distancesaved:
The Time-Distance between Fields to be saved.
tminimum= TMIN, tmaximum= TMAX:
The minimum and maximum Time to simulate. gd1 will simulate a minimum simulation Time of TMIN and a maximum one of TMAX.
- For a broadband Computation: If after TMIN no Power is flowing through any Port, the Simulation is stopped.
- For a monochromatic Computation (risetime /= 0): If after TMIN the Power flowing through all Ports is stationary, the Simulation is stopped.
No matter what the Status of the Fields in the computational Volume is, after a simulation Time of TMAX, the Simulation will be stopped.
decaytime= OOALPHA:
Specification of artificial Losses in the computational Volume.
- OOALPHA:
  Time (in Seconds) that the Fields (both E and B) decay by a Factor of 1/e.
The Reason for this Parameter is as follows: single.gd1 calculates mostly in single Precision, with a relative Accuray of its internal Values of $10^{-7}$ for most Machines. With this Machine Accuracy, it is not possible to calculate the Decay of high Q-Structures. If you would fill your Volume not with Vacuum but with a Dielectric with a very low Conductivity $\kappa$ , the Program would attempt to scale in every Timestep the electric Field with a Factor of 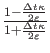$\frac{1- \frac{\Delta t \kappa}{2 \varepsilon}} {1+ \frac{\Delta t \kappa}{2 \varepsilon}}$ . For low Values of $\kappa$ this Factor is so near to One that it cannot be represented in single Precision as distinct from One.
With the specification of decaytime, the Fields (both E and B) in the entire Volume are scaled by such a Factor, that after a simulation Time of OOALPHA the Fields have decayed by a Factor of 1/e.
If you have to calculate the Scattering Parameters of a Resonator with a known (not too low) internal Q-value, e.g. greater than 1000, you can specify artificial Losses with this Keyword and gd1 or single.gd1 together with gd1.pp will calculate the proper scattering Parameters.
amptresh= TRESH:
The Treshold Value for exiting the FDTD-Loop when performing a broadband Computation: When all Port-Amplitudes have decayed down to TRESH times the maximum of all monitored Modes at all Times before, the Computation stops.
dtsafety:
The safety Factor for the Timestep.
gd1 computes the largest stable Timestep as
$dtmax= \sqrt{\frac{4} {''highest\; eigenvalue\; of\; the\; closed\; volume''}}$
This is normally reliable and gives the minimum Number of Timesteps required for a wanted simulation Time. If for some Reason you want to use a different Timestep, you may change the Timestep by changing dtsafety. The used Timestep is
dt = dtsafety * dtmax .
ndt:
This enforces the used Timestep "dt" to be such that "dt" is smaller than the normally used Timestep and that an integer multiple of "dt" gives the Value of "ndt".
___stopafter:
Enforces a Stop after computing so far. Not very useful. We needed it once.
___evmax:
If specified, ignores the Result of the Estimation of the highest Eigenvalue of the Curl Curl Operator. The largest stable Timestep is then computed not from that Estimate but from a highest Eigenvalue being ___evmax. NOT USEFUL. This is avaiable to test that the Results of parallel and serial Computations are bitwise identical.
___dt:
If specified, uses that Value as the Timestep. NOT USEFUL.

Example The following specifies that we want to simulate a minimum Timespan of 100 Periods of a Frequency of 1 GHz. We are absolutely shure that after a Timespan of 1000 Periods the Fields have decayed sufficiently, and we want to store the Fields between 10 Periods and 20 Periods, in a Distance of 1/2 Period.

  define(FREQ, 1e9)
  tmin=  100/FREQ, tmax= 1000/FREQ
  firstsaved= 10/FREQ, lastsaved=  20/FREQ
  distance=   1/2/FREQ

-fdtd,-storefieldsat: When to Store

Selected Fields can be stored at selected Times. This Section triggers the writing of full Fields. If you want to monitor selected Components, or selected Fluxes, use -fmonitor or -smonitor.

 ##############################################################################
 # Flags: nomenu, noprompt, nomessage,                                        #
 ##############################################################################
 # Section: -storefieldsat                                                    #
 ##############################################################################
 # name  = noname-0001                                                        #
 # whattosave= both                     -- e-fields, h-fields, both, clouds,  #
 #                                      --     jimpedance                     #
 # firstsaved   = undefined                                                   #
 # lastsaved    = undefined                                                   #
 # distancesaved= undefined                                                   #
 ##############################################################################
 # doit, list, ?, return, help                                                #
 ##############################################################################

name:
The Name to be used to identify the stored Data later. When you enter the Name of an already defined Set, you can edit the Parameters for this already defined Set. When you specify a Name of "name= a", the saved e-Fields are accessible later in the Post-Processor under the Name "a_e_1" for the first stored Field. The first stored h-Field of the Set is accessible as "a_h_1".
whattosave:
Possible Values are e-fields, h-fields, both, clouds, jimpedance. The clouds Value is for PIC-Computations, it specifies that only the Data of free moving Charges shall be stored at the selected Times. If you have a PIC-Computation running, and you have selected one of e-fields, h-fields, both, the Data of free moving Charges are stored as well.
firstsaved:
The first Time where the Datasets shall be stored to Files.
lastsaved:
The last Time where the Datasets shall be stored to Files.
distancesaved:
The Time-Distance between Datasets to be saved.
doit:
Stores the current Data and enables the editing of the Parameters of a Set that is not yet defined (a new Set).
list:
Lists the Names of the already defined Sets.

Example The following specifies that we want to store both the electric and magnetic Fields in the Timespan of 10 Periods to 12 Periods. The Distance shall be 0.1 periods. In the Timespan between 20 Periods and 30 Periods we want to store only the electric Field. The Distance between the saved fields shall be a quarter Period.

 define(FREQ, 1e9)

 -fdtd
    -storefieldsat
      name= a, what= both
         firstsaved= 10/FREQ
         lastsaved=  12/FREQ
         distance=   0.1/FREQ
      doit

      name= b, what= e-fields
         firstsaved= 20/FREQ
         lastsaved=  30/FREQ
         distance=   0.25/FREQ
      doit

Example The following specifies that we want to store the electric Fields every 100 HF-Periods. Every 100 HF-Periods the fields shall be stored with a Time Density of 1/8 Period.

 define(FREQ, 1e9)

 -fdtd
    -storefieldsat
      do ii= 100, 1000, 100
         #
         # This 'name= a-ii' is expanded to eg. 'name= a-100'
         #
         name= a-ii, what= e-fields
            firstsaved=  ii       /FREQ
            lastsaved=  (ii+1+1/8)/FREQ
            distance=   1/8/FREQ
         doit
      enddo

-fdtd,-fexport: Text-File Export of selected Fields at selected Times

During a Time Domain Computation (also windowwake), the Fields can be stored at selected Times. The written Files can be imported by other Programs, or they can be used to create gif-Files and then mpeg-Files.

 ##############################################################################
 # Flags: nomenu, noprompt, nomessage,                                        #
 ##############################################################################
 # Section: -fexport                                                          #
 ##############################################################################
 # outfile= noname-0001
 # whattosave= e                        -- e-fields, h-fields, honmat         #
 # firstsaved   = undefined                                                   #
 # lastsaved    = undefined                                                   #
 # distancesaved= undefined                                                   #
 # bbxlow  =    -1.0000e+30, bbylow =    -1.0000e+30, bbzlow =    -1.0000e+30 #
 # bbxhigh =     1.0000e+30, bbyhigh=     1.0000e+30, bbzhigh=     1.0000e+30 #
 ##############################################################################
 # doit, ?, return, end, help                                                 #
 ##############################################################################

outfile:
The Name of the File to write the Fieldvalues to.
whattosave:
Specifies what Field shall be exported to File. If whattosave=honmat, the Values of H on electric conducting Surfaces are written in a complicated special compressed Format, which (probably) can only be read by gd1.pp's section -3dmanygifs. The File-Format is so complicated to keep the Filesizes small.
firstsaved, lastsaved, distancesaved:
The first, last Time to store the Field, and the Distance between the Times when the Field shall be stored.
bbxlow=,bbxhigh=,bbylow=bbyhigh=,bbzlow=,bbzhigh=:
Specifies the Coordinates of a bounding Box. Only the Fields that lie within the Box are written.
doit:
While the Time Domain Computation is running, the Exportfiles are written. The Format of the Files should be self-explanatory.

Example The following Inputfile is for performing a Wakepotential Computation with a moving Mesh Window. During the Time Domain Computation, the magnetic Fields on the Boundaries shall be exported as ASCII-Files.

 define(STPF, 0.5) define(NP, 4) define(RADIUS, 1+1) define(GAP, 0.5)
 define(PERIODE, 0.6) define(BEAMR, RADIUS/2) define(STPSZE, SIGMA/10/STPF)

 define(DRADIUS, 2*STPSZE )
 define( ZLOW, -(NP*PERIODE+BEAMR)/2 )
 define( ZHIGH, (NP*PERIODE+BEAMR)/2 )
 -general
    outfile= /tmp/UserName/resultfile
    scratch= /tmp/UserName/scratch

 -mesh
    pxlow= -(RADIUS+DRADIUS), pxhigh= (RADIUS+DRADIUS)
    pylow= -(RADIUS+DRADIUS), pyhigh= (RADIUS+DRADIUS)
    pzlow= ZLOW, pzhigh= ZHIGH
 define(PZLOW, ZLOW)
 define(PZHIGH, ZHIGH)

   pxlow= 0, cxlow= mag
   pylow= 0, cylow= mag
   spacing= STPSZE

 ############
 -brick, material 1, volume (-INF, INF, -INF, INF, -INF, INF), doit

 do ip= -(NP-1)/2, (NP-1)/2, 1
    -gccylinder
       material= 0, radius= RADIUS, length= GAP
       origin= (0,0,ip*PERIODE-GAP/2)
       direction= (0,0,1)
 show= later
       doit
 enddo

 -gccylinder
    material= 0, radius= BEAMR, length= INF
    origin= ( 0, 0, -INF/2 ), direction= ( 0, 0, 1 )
# show= all
    doit

 #####
 -volumeplot, scale 1.8, plotopts -geometry 600x550+10+10, doit

 ####
  -lcharge
    sigma= 0.1, charge= 1e-12, xposition= 0, yposition= 0
    #
    # The following large Value for shigh is chosen for getting a Movie
    # of the full Structure.
    # 
    shigh= ZHIGH-ZLOW

   define(NDT, 0.5 * SIGMA / @clight)
 -fexport
    outfile= /tmp/UserName/H-onmat-
    what= honmat
    firstsaved= 1e-20, lastsaved= 1e20
    distancesaved= NDT
    bbxlow= 0, bbxhigh= INF
    bbylow= 0, bbyhigh= INF
    bbzlow= PZLOW+2*STPSZE, bbzhigh= PZHIGH-2*STPSZE
    doit

 -windowwake,
     doit
 end
#####################

The following is Input for gd1.pp to read the Files and create many gifs from them. From the gifs, a mpeg File is created and displayed.

# Input for gd1.pp:

 -3dmanygifs
   1stinfile= /tmp/UserName/H-onmat--000000001.gz
   outfiles= /tmp/UserName/absh-
## uptonfiles= 10
#   what= abs
   what= logabs
   uptonfiles= 1e9
   xrot= -30, yrot= 40
   doit

 system( mpeg_encode ./gdfidl.3dmanygifs-mpeg_encode-params )
 system( mpeg_play -dither color fexported.mpg )

-fdtd,-smonitor: Monitoring of scalar Quanitities

During a Time Domain Computation (with a static Mesh, i.e. not windowwake), the scalar Field Quantities can be monitored.

 ##############################################################################
 # Flags: nomenu, noprompt, nomessage,                                        #
 ##############################################################################
 # Section: -smonitor                                                         #
 ##############################################################################
 # name  = noname-001                                                         #
 # whattosave= convectioncurrent                                              #
 #                       -- convectioncurrent, displacementcurrent            #
 #                       -- magneticflux                                      #
 #                       -- poyntingflux, ppclouds, pnclouds                  #
 #    normal= z, cutat= undefined                                             #
 #    xlow=      -1.0e+30    , xhigh=       1.0e+30                           #
 #    ylow=      -1.0e+30    , yhigh=       1.0e+30                           #
 #    zlow=      -1.0e+30    , zhigh=       1.0e+30                           #
 ##############################################################################
 # doit, list, ?, return, help                                                #
 ##############################################################################

name:
The Name to give to the scalar Quantity.
whattosave:
Specifies what scalar Quantity shall be monitored.
normal:
The Plane Normal of the Plane Section over which the Field shall be integrated to give the scalar Quantity.
cutat:
The Coordinate Value of the Plane in which the Plane Section is lying, over which the scalar Quantity shall be integrated.
bbxlow=,bbxhigh=,bbylow=bbyhigh=,bbzlow=,bbzhigh=:
Specifies the Coordinates of a bounding Box. Only the fields that lie within the Box are integrated.
doit:
The Parameters are saved, the Parameters of a next scalar Quantity can be entered.

-fdtd,-fmonitor: Monitoring of Field Quanitities

During a Time Domain Computation (with a static Mesh, i.e. not windowwake), selected field Quantities can be monitored.

 ##############################################################################
 # Flags: nomenu, noprompt, nomessage,                                        #
 ##############################################################################
 # Section: -fmonitor                                                         #
 ##############################################################################
 # name  = noname-001                                                         #
 # whattosave= ecomponents                                                    #
 #                       -- ecomponents, hcomponents                          #
 #    position= ( 0.0, 0.0, 0.0 )                                             #
 ##############################################################################
 # doit, list, ?, return, help                                                #
 ##############################################################################

name:
The Name to give to the Field Quantity.
whattosave:
Specifies what Field Quantity shall be monitored.
position:
The cartesian Components of the Location where the Field Quanity shall be monitored.
doit:
The Parameters are saved, the Parameters of a next Field Quantity can be entered.

-fdtd,-pmonitor: Monitoring of Power Quanitities

During a Time Domain Computation (with a static Mesh, i.e. not windowwake), selected Power Quantities can be monitored.

 ##############################################################################
 # Flags: nomenu, noprompt, nomessage,                                        #
 ##############################################################################
 # Section: -PMonitor                                                         #
 ##############################################################################
 # name = noname-001                                                          #
 # whattosave= pdielectrics                                                   #
 #                       -- ( pdielectrics | energy )                         #
 #    xlow=      -1.0e+30    , xhigh=       1.0e+30                           #
 #    ylow=      -1.0e+30    , yhigh=       1.0e+30                           #
 #    zlow=      -1.0e+30    , zhigh=       1.0e+30                           #
 #    stride= 10                                                              #
 ##############################################################################
 # doit, list, ?, return, help                                                #
 ##############################################################################

name:
The Name to give to the Power Quantity.
whattosave:
Specifies what Power Quantity shall be monitored.
xlow=, xhigh=, ylow=, yhigh=, zlow=, zhigh= :
Specifies the Coordinates of a bounding Box. Only the Fields that lie within the Box are integrated.
doit:
The Parameters are saved, the Parameters of a next Power Quantity can be entered.

gd1.pp

gd1.pp is the Postprocessor. gd1.pp loads the Data that is computed by gd1 and displays it. gd1.pp also computes Integrals over Fields, like Wall Losses and Voltages. Together with the Macro Facility, this allows comfortable Computation of Figures of Merit like Q-Values and Shunt-Impedances.
A Special Section (-sparameter) computes Scattering Parameters from the Amplitudes of Port-Modes that were computed and stored by gd1.
Wakepotentials and Impedances are computed in the Section -wakes.
TouchStone-Files containing Scattering Matrices may be created in the Section -totouchstone.

Before you can do anything useful, you have to specify from what Database gd1.pp shall take the Fields from. Therefore the first Thing you do is: enter the Section -general.

-base

This is the Base Section of gd1.pp.

 ##############################################################################
 # Flags: nomenu, noprompt, nomessage,                                        #
 ##############################################################################
 # Section: -base                                                             #
 #  VshzpnIb 210909                                                           #
 ##############################################################################
 # -general         -- Define Database                                        #
 # -3darrowplot     -- Field Plots, Material Plot                             #
 # -lineplot        -- Lineplot of Field Components,                          #
 # -glineplot       -- Lineplot of Field Comp along gline,                    #
 # -2dplot          -- Aquivalue Plot of a Component on a Plane.              #
 # -energy          -- Compute stored Energy                                  #
 # -lintegral       -- Compute Voltages                                       #
 # -wlosses         -- Compute Wall Losses                                    #
 # -dlosses         -- Compute dielectric Losses                              #
 # -flux            -- Compute Fluxes through rectangular Areas               #
 # -clouds          -- Properties of free moving Clouds                       #
 # -sparameters     -- Analyses Time History of Port Mode Amplitudes          #
 # -material        -- Specify Conductivities for Loss Computations           #
 # -wakes           -- Wakepotentials, Impedances                             #
 # ***** Miscellanea ******                                                   #
 #  -totouchstone   -- Convert fri-data to touchstone Form                    #
 #  -combine        -- Combines Scattering Parameters                         #
 #  -pcombine       -- Combines E & H to Poynting Field.                      #
 #  -smonitor       -- Display and fft smonitor Data                          #
 #  -fmonitor       -- Display and fft fmonitor Data                          #
 #  -pmonitor       -- Display pmonitor Data                                  #
 #  -voltages       -- Display and fft Voltages Data                          #
 #  -fexport        -- Export 3D Field Data                                   #
 #  -2dmanygifs     --                                                        #
 #  -3dmanygifs     --                                                        #
 #  -debug          -- Specify Debug Levels                                   #
 #                                                                            #
 ##############################################################################
 # ?, help, end, ls                                                           #
 ##############################################################################

-general:
Branches to the -general Section, where you load the Database, where gd1 has written its Data to.
-3darrowplot:
Branches to the Section 3darrowplot, where you can plot 3D-Fields together with the Material-Boundaries.
You can also plot the computed Portmodes that were used in a Time-Domain Computation.
-lineplot:
Branches to the Section lineplot, where you can plot selected Components of 3D-Fields along selected Lines. The Direction of these Lines must be in x-, y- or z-Direction.
-glineplot:
Branches to the Section glineplot, where you can plot selected components of 3D-Fields along selected Lines in arbitrary Direction.
-2dplot:
Branches to the Section 2dplot, where you can plot selected Components of 3D-Fields over a Plane as an Aequivalue Plot.
-energy:
Branches to the Section -energy, where you can compute the stored Energy in resonant or time dependent Fields.
-lintegral:
Branches to the Section lintegral, where you can compute Line Integrals of Fields.
-wlosses:
Branches to the Section -wlosses, where you can compute Wall Losses from magnetic Fields via the perturbation Formula.
-dlosses:
Branches to the section -dlosses, where you can compute dielectric Losses from electric or magnetic Fields via the perturbation Formula.
-flux:
Branches to the Section -flux, where you can compute the Flux of a Field through a rectangular Area.
-clouds:
Branches to the Section -clouds, where you can analyse results of a PIC Computation.
-sparameters:
Branches to the Section -sparameters, where you can compute and Plot the scattering Parameters from the Time-Domain Data that were computed by gd1.
-material:
Branches to the Section -material, where you may change the Conductivities of electric Materials. These Conductivities are used for the perturbation Formula that is applied in the Section -wlosses.
-wakes:
Branches to the Section -wakes, where you can compute longitudinal and transverse Wakepotentials from Data that were recorded by gd1 during a Time Domain Computation with a relativistic Charge.
-totouchstone:
Branches to the Section -totouchstone, where you may combine selected scattering Parameters to a full scattering Matrix which is then stored in TouchStone-Format.
-combine:
Branches to the Section -combine, where you can combine scattering Parameters of different Devices to get the scattering Parameters of a combined Device.
-smonitor:
Branches to the Section -smonitor, where you can analyse Results which were recorded via -smonitor in a Time-Domain Computation.
-fmonitor:
Branches to the Section -fmonitor, where you can analyse Results which were recorded via -fmonitor in a Time-Domain Computation.
-pmonitor:
Branches to the Section -pmonitor, where you can analyse Results which were recorded via -pmonitor in a Time-Domain Computation.
-fexport:
Branches to the Section fexport, where you can export 3DFields to ASCII Files.
-2dmanygifs, -3dmanygifs:
Allows Creation of Sets of GIF Files from Data exported from a Time Domain Computation via -fexport.
-debug:
This Section is for debugging GdfidL.

-general

Here you specify what Resultfile shall be processed and where Scratchfiles shall be written to.

 ##############################################################################
 # Flags: nomenu, noprompt, nomessage,                                        #
 ##############################################################################
 # Section: -general                                                          #
 ##############################################################################
 # infile= ./results                                                          #
 # scratchbase= /scratch/wb//gdfidl-scratch-pid=000014263-                    #
 # text( 1)=                                                                  #
 ##############################################################################
 # 2dplotopts= -geometry 690x560+10+10                                        #
 #  linecolor= 0              -- 0: foreground, 3: yellow                     #
 #  foreground= black         -- black, white                                 #
 #  background= white         -- blue, white, black                           #
 # showtext     = yes         -- (yes | no)                                   #
 # onlyplotfiles= no          -- (yes | no)                                   #
 # nrofthreads= 20            -- SMP: Nr of Threads.                          #
 ##############################################################################
 # ?, return, end, help, ls                                                   #
 ##############################################################################

infile:
The Name of the Resultfile from gd1. "infile= @last" is special: The Name of the last computed "outfile" is taken (this Value is read from the File $HOME/name.of.last.gdfidl.file)
scratchbase:
The Base Name of Scratchfiles that gd1.pp needs for its Operation. These will be mainly Plotfiles. If you have an Environment Variable TMPDIR set, gd1.pp will take as default Value set scratchbase to the String
```
    $TMPDIR/gdfidl-scratch-pid=XXXXX-
```
Here $TMPDIR is the Value of the Environment Variable TMPDIR, and XXXXX is the Number of the Process-ID of gd1.pp.
text(*)= This Annotation-Text is plotted together with the Plots.
syntax:
text()= ANY STRING, NOT NECESSARILY QUOTED
or
text(NUMBER)= ANY STRING, NOT NECESSARILY QUOTED
- ANY STRING, NOT NECESSARILY QUOTED:
  The String to be included in the Plots.
- NUMBER:
  Optional. The Line-Number, where the Text shall be plotted.
In the first Case, without NUMBER, the String following text()= is placed in the next free Line. In the Case with NUMBER, it is guaranteed, that the String is placed in the NUMBER.st Line. You can specify up to 20 Annotation-Strings, the maximum Length of each Annotation-String is 80 Characters.
When a new Database is specified, the Values of text are overwritten by the Values that are found in the Database.
2dplotopts= ANY STRING CONTAING OPTIONS FOR mymtv2:
gd1.pp does not display the Data itself, but writes a Datafile for mymtv2 (1D and 2D Data) and starts mymtv2 to display these Data.
Useful Options are:
- -geometry X11-GEOMETRY Initial geometry for the X11 window of mymtv2.
plotopts= ANY STRING CONTAING OPTIONS FOR gd1-3dplot:
gd1.pp does not display the Data itself, but writes a Datafile for gd1.3dplot (3D Data) and starts gd1.3dplot to display these Data.
Useful Options are:
- -geometry X11-GEOMETRY Initial geometry for the X11 window of gd1.3dplot.
showtext= [yes|no]:
This flags, whether the Annotation-Text shall appear in the Plots.
onlyplotfiles= [yes|no]:
This flags, whether Plotfiles shall be written AND mymtv2 or gd1.3dplot shall be started to display them on a X11 Display, or whether only the Plotfiles shall be produced.

Example The following specifies that we want to work with the Data that is generated by the last Run of gd1. We want to have the Scratchfiles written into the Directory '/tmp/garbage/' and there the Files shall be called 'delete-me-*'. We want to have mymtv2 started with an X11-geometry of 800x600. We want to have gd1.3dplot started with an X11-geometry of 1024x768.

 -general
    infile= @last
    scratchbase= /tmp/garbage/delete-me-
    2dplotopts= -geometry 800x600
    plotopts= -geometry 1024x768

-3darrowplot: Plots 3D Fields together with the Material Boundaries.

This Section plots 3D electric or magnetic Fields. Also Portmodes can be plotted.

 ##############################################################################
 # Flags: nomenu, noprompt, nomessage,                                        #
 ##############################################################################
 # Section: -3darrowplot                                                      #
 ##############################################################################
 # symbol      = e_1                                                          #
 # quantity    = e                                                            #
 # solution    = 1                                                            #
 #    phase    = 45.0                   -- Only for Portmodes                 #
 # arrows      = 10000                                                        #
 # lenarrows   = 2.0                                                          #
 # maxlenarrows= 2.0                                                          #
 #   fcolour   = 4                                                            #
 # materials   = yes                    -- (yes | no)                         #
 # dielectrics = yes                    -- (yes | no)                         #
 # fonmaterials= yes                    -- (yes | no)                         #
 #    logfonmat= no                     -- (yes | no)                         #
 #    fmaxonmat= auto                                                         #
 # jonmaterials= no                     -- (yes | no)                         #
 # scale       = 2.80                                                         #
 # fscale      = auto                                                         #
 # nlscale     = no, nlexp= 0.30                                              #
 # eyeposition = ( -1.0, -2.30, 0.50 )                                        #
 # bbxlow = -1.0000e+30,    bbylow = -1.0000e+30,    bbzlow = -1.0000e+30     #
 # bbxhigh= 1.0000e+30,     bbyhigh= 1.0000e+30,     bbzhigh= 1.0000e+30      #
 # rotx   = 0.0000,         roty   = 0.0000,         rotz   = 0.0000          #
 # clouds = yes     -- Show Clouds                                            #
 ##############################################################################
 # plotopts= -geometry 800x668+410+40 -noclip                                 #
 # showtext     = yes                   -- (yes | no)                         #
 # showlines    = no                    -- (yes | no)                         #
 # onlyplotfiles= no                    -- (yes | no)                         #
 ##############################################################################
 # @absfmax:  undefined       -- of fonmat or jonmat.                         #
 # @farrowmax:  undefined     -- Value of largest Arrow.                      #
 ##############################################################################
 # doit, ?, return, end, help, ls                                             #
 ##############################################################################

symbol= QUAN_ISOL:
This is the full Name of the Symbol to be processed.
quantity= QUAN:
This is the first Part of the "symbol".
solution= ISOL:
This is the last Part of the "symbol", the Index of the "symbol".
component:
Possible Values are x,y,z,all. Only the selected Component will be plotted.
phase:
This Parameter is used only when you want to plot the Fields of portmodes. This specifies the Phase of the Phasor to be shown. This seldom changes the Plot, as seldom the Portmodes are really Complex.
arrows:
The Arrows that make up the Plot are distributed equidistant over the whole computational Volume. The Number of Positions where an Arrow is possible is given here.
lenarrows:
The relative Length of the Arrows that make up the Plot. If lenarrows= 1, the Arrows are scaled such, that for an homogeneous Field the Tip of one shown Arrow is just behind the Bottom of the next Arrow.
maxlenarrows:
No Arrow shall be larger than this Value.
This is useful for Fields where a strong Field Concentration happens, e.g. Wakefields.
fcolour= :
The Colour Number of the Field Arrows.
materials= :
When yes, the Material Boundaries are plotted together with the Fields.
dielectrics= :
When dielectrics= no, Material Boundaries between dielectrics will not be shown.
jonmaterials= : (Joules on Materials)
A Flag that specifies whether the Colours of Material Boundaries shall be encoding the absorbed Energy in Materials with type= impedance.
fonmaterials= : (Fields on Materials)
A Flag that specifies whether the Colours of Material Boundaries shall be encoding the Field values near these Material Boundaries.
logfonmat= :
A Flag that specifies whether the Colours shall be assigned proportional to the logarithm of the Field value.
maxfonmat= :
What Value shall be used as the largest Field on the Material Patches. No further Scaling happens. This is useful for generating Movies, where every frame of the Movie should have the same Colour Encoding.
scale= SCALE:
The initial zoom Factor of the resulting Plot.
fscale:
If a Value $\ne$ auto is specified, the Vectorfield is scaled by this Value. No further Scaling happens. This is useful for generating Movies, where every frame of the Movie should be scaled by the same Factor.
nlscale, nlexp:
If nlscale= yes, the Size of Field Arrows are proportional to the Amplitude of the Field to the Power of nlexp.
eyeposition= (XEYE, YEYE, ZEYE):
This specifies the initial Eyeposition for the 3D Plot that will be produced. As soon as the Plot appears, you can interactively change the Eyeposition with the Buttons of gd1.3dplot, but for a complex Geometry, this may take some Time.
bbxlow=,bbxhigh=,bbylow=bbyhigh=,bbzlow=,bbzhigh=:
Specifies the Coordinates of a Bounding Box. Only the Material-Boundaries and the Field-Arrows that lie within the Box are plotted.
rotx= PhiX, roty= PhiY, rotz= PhiZ:
This specifies the Parameters of an additional Rotation Matrix. The Data is rotated around the x-Axis by an angle of PhiX, then the Result is rotated around the y-Axis by an angle of PhiY, and finally the Result is rotated around the z-Axis by an angle of PhiZ.
clouds= :
Selects, whether the Position free moving Charges shall be plotted together with the Field.
plotopts= ANY STRING CONTAING OPTIONS FOR gd1-3dplot:
gd1.pp does not display the Data itself, but writes a Datafile for gd1.3dplot (3D Data) and starts gd1.3dplot to display these Data.
Useful Options are:
- -geometry X11-GEOMETRY Initial geometry for the X11 window of gd1.3dplot.
showtext= [yes|no]:
This flags, whether the Annotation-Text shall appear in the Plots.
showlines= :
If yes, thin Lines are plotted around the material Patches, indicating the used Discretisation.
onlyplotfiles= [yes|no]:
This flags, whether Plotfiles shall be written AND mymtv2 or gd1.3dplot shall be started to display them on a X11 Display, or whether only the Plotfiles shall be produced.
doit:
The selected symbol is loaded from the database, the Plotfile is generated, gd1.3dplot is started to display the Plotfile.

Example To generate a Plot of the first electric Field found in the Database, we say:

   symbol= e_1
   doit

Example To generate a Plot of the real Part of the fourtht complex electric Field found in the Database, with the Colours of the material Patches showing the Field strength at the Material Boundaries, we say:

   symbol= ere_4
   fonmat= yes
   doit

 # only the Material Plot, without the Field-Arrows:
 lena 1e-6
   doit

**Figure 2.1:** Above: Resulting Plot, with Field Arrows, and Material Patches coloured according to the Field Strength at Material Boundaries. Below: The same Plot, without Field Arrows.
$\begin{figure}\centerline{ \quad \quad \psfig{figure=fonmat-eq-yes.ps,width=10cm... ...width=10cm,bbllx=20pt,bblly=232pt,bburx=582pt,bbury=802pt,clip=} }\end{figure}$

Example A Plot of the absorbed Energy in Materials with type=impedance: In the first Step, we compute the Time Domain Fields with gd1:

 gd1 < DDBA_simple_button_racetrack_no_cavity_no_recess.gdf

That Inputfile specifies all metallic Materials as of type=impedance.

 -material
   material= 3, type= impedance, kappa= 1.3514e6 # button
   material= 5, type= impedance, kappa= 1.82e7   # pin
   material= 6, type= impedance, kappa= 1.3889e6 # anulus
   material= 7, type= impedance, kappa= 4.561e7  # coax pin
   material= 8, type= impedance, kappa= 1.35e6   # block
   material= 9, type= impedance, kappa= 1.59e7   # coax outer

Fields at selected Times are stored.

    # Store the e-Fields at selected Times.
    #     This will then also store the deposited Energy in
    #     'type= impedance'.
    #  gd1.pp: -3darrow, jonmat= yes, symbol= Bla_e_1, doit
    #
    -storefieldsat
        name= Bla, what= e
           firstsaved= 0.1 / @clight
           lastsaved= INF
           distance= 0.1 / @clight
        doit

After the Time Domain Computation has finished, we start gd1.pp with the Input:

    -general, infile= @last
    -3da
        jonmat= yes
        arrows= 1, lena= 1e-7  # No Arrows shown
        symbol= Bla_e_3, doit

The resulting Plot of the absorbed Energy is shown in Figure 2.2.

**Figure 2.2:** The coloured Material-Patches encode the absorbed Energy in the Materials with type=impedance.
$\begin{figure}\epsfig{figure=jonmat-example.ps,width=18cm,bbllx=0pt,bblly=0pt,bburx=747pt,bbury=554pt,clip=}\end{figure}$

-lineplot: Plots a Field Component along an Axis.

 ##############################################################################
 # Flags: nomenu, noprompt, nomessage,                                        #
 ##############################################################################
 # Section: -lineplot                                                         #
 ##############################################################################
 # symbol    = e_1                                                            #
 # quantity  = e                                                              #
 # solution  = 1                                                              #
 # component = z                                                              #
 #    phase  =       45.0               -- Only for Portmodes                 #
 #                                                                            #
 # direction = z                                                              #
 # startpoint= ( 0.0, 0.0, -1.0e+30 )                                         #
 ##############################################################################
 # 2dplotopts= -geometry 690x560+10+10                                        #
 #  linecolor= 0              -- 0: foreground, 3: yellow                     #
 #  foreground= black         -- black, white                                 #
 #  background= white         -- blue, white, black                           #
 # showtext     = yes         -- (yes | no)                                   #
 # onlyplotfiles= no          -- (yes | no)                                   #
 ##############################################################################
 # doit, ?, return, end, help, ls                                             #
 ##############################################################################

symbol= QUAN_ISOL:
This is the full Name of the Symbol to be processed.
quantity= QUAN:
This is the first Part of the "symbol".
solution= ISOL:
This is the last Part of the "symbol", the Index of the "symbol".
component= [x|y|z|]:
The wanted Component of the 3D-Field or Portmode to be plotted.
direction= [x|y|z]:
The Direction along which the Component shall be plotted.
startpoint= (X0, Y0, Z0):
The Startpoint from which the Component shall be plotted.
2dplotopts= ANY STRING CONTAING OPTIONS FOR mymtv2:
gd1.pp does not display the Data itself, but writes a Datafile for mymtv2 (1D and 2D Data) and starts mymtv2 to display these Data.
Useful Options are:
- -geometry X11-GEOMETRY Initial geometry for the X11 window of mymtv2.
showtext= [yes|no]:
This flags, whether the Annotation-Text shall appear in the Plots.
onlyplotfiles= [yes|no]:
This flags, whether Plotfiles shall be written AND mymtv2 or gd1.3dplot shall be started to display them on a X11 Display, or whether only the Plotfiles shall be produced.
doit:
The selected Symbol is loaded from the Database, the Plotfile is generated, mymtv2 is started to display the plotfile.

Example To specify the last computed Database as the Database, then to generate a Plot of the x-Component of the electric Field of the third Field in the Database, starting from the lowest z-Coordinate in the Grid, up to the highest z-Coordinate at the Position (x,y)= (0,0), we say (using Abbreviations):

 -gen, i @last
 -linepl, sym e_3, comp x, dir z, sta (0,0,@zmin), do

In full Glory, without Abbreviations, this is:

 -general
    infile= @last
 -lineplot
    symbol= e_3
    component= x
    direction= z
    startpoint= ( 0, 0, @zmin )
  doit

-glineplot: Plots a Field Component along a Line.

 ##############################################################################
 # Flags: nomenu, noprompt, nomessage,                                        #
 ##############################################################################
 # Section: -glineplot                                                        #
 ##############################################################################
 # symbol    = e_1                                                            #
 # quantity  = e                                                              #
 # solution  = 1                                                              #
 #                                                                            #
 # startpoint= ( 0.0, 0.0, -1.0e+30 )                                         #
 # direction = ( undefined, undefined, undefined )                            #
 ##############################################################################
 # 2dplotopts= -geometry 690x560+10+10                                        #
 #  linecolor= 0              -- 0: foreground, 3: yellow                     #
 #  foreground= black         -- black, white                                 #
 #  background= white         -- blue, white, black                           #
 # showtext     = yes         -- (yes | no)                                   #
 # onlyplotfiles= no          -- (yes | no)                                   #
 ##############################################################################
 ##############################################################################
 # @gvreal= undefined       @gvimag= undefined      @gvabs= undefined         #
 ##############################################################################
 # doit, ?, return, end, help, ls                                             #
 ##############################################################################

symbol= QUAN_ISOL:
This is the full Name of the Symbol to be processed.
quantity= QUAN:
This is the first Part of the "symbol".
solution= ISOL:
This is the last Part of the "symbol", the Index of the "symbol".
startpoint= (X0, Y0, Z0):
The Position from where the Lineplot shall be started. That Point must lie within the computational Volume.
direction= ( Xn, Yn, Zn ):
The Direction of the Line along which the Plot shall be generated.
2dplotopts= ANY STRING CONTAING OPTIONS FOR mymtv2:
gd1.pp does not display the Data itself, but writes a Datafile for mymtv2 (1D and 2D Data) and starts mymtv2 to display these Data.
Useful Options are:
- -geometry X11-GEOMETRY Initial geometry for the X11 window of mymtv2.
showtext= [yes|no]:
This flags, whether the Annotation-Text shall appear in the Plots.
onlyplotfiles= [yes|no]:
This flags, whether Plotfiles shall be written AND mymtv2 or gd1.3dplot shall be started to display them on a X11 Display, or whether only the Plotfiles shall be produced.
doit:
The Plot is generated. Only the Component of the Field in direction will be plotted. The Component is plotted as a Function of u.
The Lineplot is performed a Line

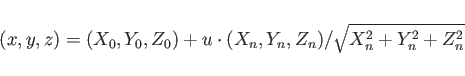
$\begin{displaymath} (x,y,z) = (X_0,Y_0,Z_0) + u \cdot (X_n, Y_n, Z_n) / \sqrt{X_n^2+Y_n^2+Z_n^2} \end{displaymath}$

As a Sideeffect, the complex Voltage as seen by a Particle is integrated.

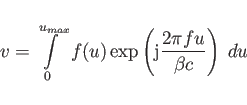
$\begin{displaymath} v = \int\limits_0^{u_{max}} f(u) \exp\left({\rm j}\frac{ 2 \pi f u } { \beta c } \right) \; du \end{displaymath}$

$\beta$ is fixed to $\beta=1$ , and is the Frequency of the resonant Field. The Result of the Integration is shown in the Menu. The Value of the Integral is also accessible as the symbolic Variables @gvreal, @gvimag, @gvabs.

-2dplot: Plot a Field Component on a Plane

 ##############################################################################
 # Flags: nomenu, noprompt, nomessage,                                        #
 ##############################################################################
 # Section: -2dplot                                                           #
 ##############################################################################
 # symbol    = e_1                                                            #
 # quantity  = e                                                              #
 # solution  = 1                                                              #
 #                                                                            #
 # component = z                        -- What Component to be plotted.      #
 # normal    = z                        -- The Plane Normal of the Cut-Plane. #
 # cutat     = undefined                -- The Coordinate of the Cut-Plane.   #
 # ncontourlines= 30                    -- The Number of Contourlines.        #
 # fscale    = auto                                                           #
 #                                                                            #
 ##############################################################################
 # 2dplotopts= -geometry 690x560+10+10                                        #
 #  linecolor= 0              -- 0: foreground, 3: yellow                     #
 #  foreground= black         -- black, white                                 #
 #  background= white         -- blue, white, black                           #
 # showtext     = yes         -- (yes | no)                                   #
 # onlyplotfiles= no          -- (yes | no)                                   #
 ##############################################################################
 # doit, ?, return, end, help                                                 #
 ##############################################################################

symbol= QUAN_ISOL:
This is the full Name of the Symbol to be processed.
quantity= QUAN:
This is the first Part of the "symbol".
solution= ISOL:
This is the last Part of the "symbol", the Index of the "symbol".
component:
What Component of the Field shall be plotted.
normal:
The Plane Normal of the Plane to plot the Component in.
cutat:
The Coordinate of the Plane to plot the Component in.
ncontourlines:
The Number of Contourlines to plot.
fscale:
The Scale Factor to apply to the Field before it is plotted. Only the Contourlines between -1 and +1 of the scaled Field will be plotted. Useful for generating Movies.
2dplotopts= ANY STRING CONTAING OPTIONS FOR mymtv2:
gd1.pp does not display the Data itself, but writes a Datafile for mymtv2 (1D and 2D Data) and starts mymtv2 to display these Data.
Useful Options are:
- -geometry X11-GEOMETRY Initial geometry for the X11 window of mymtv2.
plotopts= ANY STRING CONTAING OPTIONS FOR gd1-3dplot:
gd1.pp does not display the Data itself, but writes a Datafile for gd1.3dplot (3D Data) and starts gd1.3dplot to display these Data.
Useful Options are:
- -geometry X11-GEOMETRY Initial geometry for the X11 window of gd1.3dplot.
showtext= [yes|no]:
This flags, whether the Annotation-Text shall appear in the Plots.
onlyplotfiles= [yes|no]:
This flags, whether Plotfiles shall be written AND mymtv2 or gd1.3dplot shall be started to display them on a X11 Display, or whether only the Plotfiles shall be produced.
doit:
The selected Symbol is loaded from the database, the Plotfile is generated, mymtv2 is started to display the Plotfile.

-energy: Compute Energy in E or H Fields

In this Section you may compute the stored Energy for an electric or magnetic Field. The Result of that Computation is stored in symbolic Variables that may be used e.g. for Computation of user defined figures of Merit.

 ##############################################################################
 # Flags: nomenu, noprompt, nomessage,                                        #
 ##############################################################################
 # Section: -energy                                                           #
 ##############################################################################
 # symbol   = h_1                                                             #
 # quantity = h                                                               #
 # solution = 1                                                               #
 # bbxlow =    -1.0000e+30, bbylow =    -1.0000e+30, bbzlow =    -1.0000e+30  #
 # bbxhigh=     1.0000e+30, bbyhigh=     1.0000e+30, bbzhigh=     1.0000e+30  #
 #                                                                            #
 #                                                                            #
 # @henergy : undefined                 (symbol: undefined, m: 1)             #
 # @eenergy : undefined                 (symbol: undefined, m: 1)             #
 ##############################################################################
 # doit, ?, return, end, help, ls                                             #
 ##############################################################################

symbol= QUAN_ISOL:
This is the full Name of the Symbol to be processed.
quantity= QUAN:
This is the first Part of the "symbol".
solution= ISOL:
This is the last Part of the "symbol", the Index of the "symbol".
bbxlow=,bbxhigh=,bbylow=bbyhigh=,bbzlow=,bbzhigh=:
Specifies the Coordinates of a bounding box. Only the Fields that lie within the Box are used for integrating the Energy.
doit: Performs the Computation. The specified Field is loaded from File and its Energy density is integrated over the computational Volume.
If the integrated Field was an electric Field, the Result of the Computation is stored in the symbolic Variable @eenergy. If the integrated Field was a magnetic Field, the Result of the Computation is stored in the symbolic Variable @henergy.

The Energy for a magnetic Field is computed as:

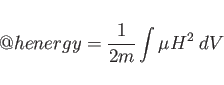$\begin{displaymath} @henergy = \frac{1}{2m} \int \mu H^2 \; dV \end{displaymath}$

(2.1)

The Energy for an electric Field is computed as:

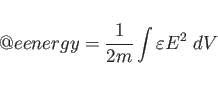$\begin{displaymath} @eenergy = \frac{1}{2m} \int \varepsilon E^2 \; dV \end{displaymath}$

(2.2)

The Time-Averaging Factor m is 2 for resonant Fields, and 1 for nonresonant Rields.

When you are computing resonant Fields without periodic Boundary Conditions, the Fields that gd1.pp processes are the electric Fields at a Time t=0 and the magnetic Fields at a Time t=T/4, where T=1/f. This means, you 'see' both, the electric and magnetic Fields at a Time where they are at a Maximum. To get the total stored Energy for resonant Fields, one has to integrate $(1/2) \mu H^2 + (1/2) \varepsilon E^2$ over the Volume at one instant Time. But E and H are not at the same Time. They are offset by T/4. The Factor of 1/m, with m=2 for resonant Fields, accounts for the Effect of integrating both the electric and magnetic Fields at their (time) Peak Values.

When you are computing time dependent Fields, the Fields that gd1.pp (normally) processes are electric and magnetic Fields at (almost) the same Time (almost, because there is a Time-Offset of half of the used Timestep, but the used Timestep is very small). For time dependent Fields, the electric and magnetic Fields are not at their Time-Peak Values, but more important, the electric and magnetic Fields are at the same Time. The stored Energy can therefore be expressed directly by integrating $(1/2) \mu H^2 + (1/2) \varepsilon E^2$ over the Volume. No factor 'm' is needed.

You cannot and do not need to specify that 'm'. gd1.pp does this for you.

Example To compute the stored Energy in the first electric Field found in the Database, we say:

 -energy, symbol= e_1, doit

-lintegral: Computes Line Integrals

This Section computes the Integral

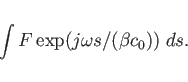
$\begin{displaymath} \int F \exp(j \omega s / (\beta c_0)) \; ds. \end{displaymath}$

 ##############################################################################
 # Flags: nomenu, noprompt, nomessage,                                        #
 ##############################################################################
 # Section: -lintegral                                                        #
 ##############################################################################
 # symbol    = e_1                                                            #
 # quantity  = e                                                              #
 # solution  = 1                                                              #
 #                                                                            #
 # direction = z                                                              #
 # component = z                                                              #
 # startpoint= ( 0.0, 0.0, -1.0e+30 )                                         #
 #    (used) : ( @x0: undefined, @y0: undefined, @z0: undefined )             #
 # length    = auto                                                           #
 #    (@length) : undefined                                                   #
 # beta      = 1.0                                                            #
 # frequency = auto                     -- [auto | Real]                      #
 ##############################################################################
 # @vreal= undefined        @vimag= undefined       @vabs= undefined          #
 ##############################################################################
 # doit, ?, return, end, help, ls                                             #
 ##############################################################################

symbol= QUAN_ISOL:
This is the full Name of the Symbol to be processed.
quantity= QUAN:
This is the first Part of the "symbol".
solution= ISOL:
This is the last Part of the "symbol", the Index of the "symbol".
direction= [x|y|z]:
The cartesian Direction along which the Integration shall be performed.
component= [x|y|z]:
The cartesian Component that shall be integrated.
startpoint= ( X0, Y0, Z0 ):
The Integration Range starts at this Position.
length:
Possible Values are auto, or a real Number.
If length= auto, the Integration is performed from the Startpoint to the End of the computational Domain (in direction-direction).
beta:
The Value of $\beta$ in the Formula $\int F \exp(j \omega s / (\beta c_0)) \; ds$ . If you are interested in computing $\int F \; ds$ , then choose beta as a very large Number, say 1e+10.
frequency:
If "auto", the Frequency is taken from the Dataset. If frequency is specified as a Number, that Value is taken for the Integrand.
doit:
The Integration is performed, the Results are shown in the Menu. The Value of the Integral is also accessible as the symbolic Variables @vreal, @vimag, @vabs. The Length of the used Integration Path is accessible as the Variable @length. The Coordinates of the used Startpoint are accessible as @x0, @y0, @z0.

-wlosses: Compute Wall Losses from H-fields

In this Section you may compute the Wall Losses that stem from the Induction of Surface Currents from magnetic Fields. This is a Power Loss Perturbation Computation.

 ##############################################################################
 # Flags: nomenu, noprompt, nomessage,                                        #
 ##############################################################################
 # Section: -wlosses                                                          #
 ##############################################################################
 # symbol    = h_1                                                            #
 # quantity  = h                                                              #
 # solution  = 1                                                              #
 # frequency = auto                     -- [auto | Real]                      #
 # bbxlow =    -1.0000e+30, bbylow =    -1.0000e+30, bbzlow =    -1.0000e+30  #
 # bbxhigh=     1.0000e+30, bbyhigh=     1.0000e+30, bbzhigh=     1.0000e+30  #
 #                                                                            #
 #                                                                            #
 # @metalpower : undefined         [VA] (symbol: undefined)                   #
 ##############################################################################
 # doit, ?, return, end, help, ls                                             #
 ##############################################################################

The Conductivities that are used in the Perturbation Formula may be changed in the Section -material. The Result of the Computation is available as the symbolic Variable @metalpower. The Wall Losses are computed as:

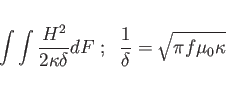
$\begin{displaymath} \int \int \frac{H^2}{2 \kappa \delta} dF \; ; \; \; \frac{1}{\delta} = \sqrt{ \pi f \mu _0 \kappa } \end{displaymath}$

The Integration is performed over all metallic Surfaces that would appear in a Plot as produced by the Section -3darrowplot. This implies, that Wall Losses are NOT computed for electric Planes of Symmetry, since the Material on the Planes of Symmetry are not shown in -3darrowplot.

symbol= QUAN_ISOL:
This is the full Name of the Symbol to be processed. This Field has to be a 3D-H-Field.
quantity= QUAN:
This is the first Part of the "symbol".
solution= ISOL:
This is the last Part of the "symbol", the Index of the "symbol".
frequency:
If "auto", the Frequency is taken from the Dataset. If frequency is specified as a Number, that Value is taken for the Integrand.
bbxlow=,bbxhigh=,bbylow=bbyhigh=,bbzlow=,bbzhigh=:
Specifies the Coordinates of a Bounding Box. Only the metallic Surfaces that lie within the Box are used for integrating the Wall Losses.
doit:
The Integration is performed, the Result is shown in the Menu. The Result is available as the Symbol @metalpower for subsequent Calculations.

-dlosses: Compute dielectric Losses

In this Section you may compute dielectric Losses. The Result of the Computation is available as the symbolic Variables @muepower, @epspower. The dielectric Losses are computed as:

For electric Fields:

$\begin{displaymath} \frac{1}{m} \int \vec{E} \cdot \kappa_e \vec{E} \; dV = {\rm @epspower \; [VA]} \end{displaymath}$

For magnetic Fields:

$\begin{displaymath} \frac{1}{m} \int \vec{H} \cdot \kappa_m \vec{H} \; dV = {\rm @muepower \; [VA]} \end{displaymath}$

The Integration is performed over the specified Volume. The time-averaging Factor m is 2 for resonant Fields, and 1 for nonresonant Fields.

 ##############################################################################
 # Flags: nomenu, noprompt, nomessage,                                        #
 ##############################################################################
 # Section: -dlosses                                                          #
 ##############################################################################
 # symbol    = h_1                                                            #
 # quantity  = h                                                              #
 # solution  = 1                                                              #
 # bbxlow =    -1.0000e+30, bbylow =    -1.0000e+30, bbzlow =    -1.0000e+30  #
 # bbxhigh=     1.0000e+30, bbyhigh=     1.0000e+30, bbzhigh=     1.0000e+30  #
 #                                                                            #
 #                                                                            #
 # @muepower : undefined               (symbol: undefined, m: 1)              #
 # @epspower : undefined               (symbol: undefined, m: 1)              #
 ##############################################################################
 # doit, ?, return, end, help, ls                                             #
 ##############################################################################

symbol= QUAN_ISOL:
This is the full Name of the Symbol to be processed. This Field has to be a 3D-Field.
quantity= QUAN:
This is the first Part of the "symbol".
solution= ISOL:
This is the last Part of the "symbol", the Index of the "symbol".
bbxlow=,bbxhigh=,bbylow=bbyhigh=,bbzlow=,bbzhigh=:
Specifies the Coordinates of a Bounding Box. Only the Fields that lie within the Box are used for integrating the Losses.
doit:
The Integration is performed, the Result is shown in the Menu. The Result is available as the Symbol @epspower or @muepower for subsequent Calculations.

-flux: Compute Flux of Fields through rectangular Areas

In this Section you may compute the Flux of a Field through a rectangular Area.

 ##############################################################################
 # Flags: nomenu, noprompt, nomessage,                                        #
 ##############################################################################
 # Section: -flux                                                             #
 ##############################################################################
 # symbol  = h_1                                                              #
 # quantity= h                                                                #
 # solution= 1                                                                #
 #                                                                            #
 # normal  = z                     -- [x|y|z]                                 #
 # cutat   = undefined             -- Coordinate of the integration Plane     #
 # xlow= undefined            , xhigh= undefined                              #
 # ylow= undefined            , yhigh= undefined                              #
 # zlow= undefined            , zhigh= undefined                              #
 #    ( used: @cutat : undefined )                                            #
 #    ( used: @xlow  : undefined        , @xhigh  : undefined )               #
 #    ( used: @ylow  : undefined        , @yhigh  : undefined )               #
 #    ( used: @zlow  : undefined        , @zhigh  : undefined )               #
 # @flux : undefined [undefined]                                              #
 ##############################################################################
 # doit, ?, return, end, help, ls                                             #
 ##############################################################################

symbol= QUAN_ISOL:
This is the full Name of the Symbol to be processed. This Field may be a 3D-E-Field or a 3D-H-Field.
quantity= QUAN:
This is the first Part of the "symbol".
solution= ISOL:
This is the last Part of the "symbol", the Index of the "symbol".
normal= [x|y|z]:
The Plane Normal of the Surface through which the Flux Integration shall be performed.
cutat= :
The "normal" Coordinate of the Area through which the Integration shall be performed.
xlow= ??, xhigh= ??, ylow= ??, yhigh= ??, zlow= ??, zhigh= ??:
The Coordinates of the rectangular Area through which the Flux Integration shall be performed.
If normal= x, the Values xlow= ??, xhigh= ?? are ignored.
If normal= y, the Values ylow= ??, yhigh= ?? are ignored.
If normal= z, the Values zlow= ??, zhigh= ?? are ignored.
The actually used Values will be slightly different from the specified ones. After doit, the actually used Values will be accessible as the symbolic Variables
@cutat, @xlow, @xhigh, @ylow, @yhigh, @zlow, @zhigh.
doit:
The Flux Integration is performed, the Result is shown in the Menu. The Result is available as the Symbol @flux for subsequent Calculations.
If the integrated Field is an electric Field, the Result is

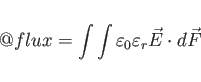
$\begin{displaymath} @flux = \int \int \varepsilon_0 \varepsilon_r \vec{E} \cdot d\vec{F} \end{displaymath}$

If the integrated Field is a magnetic Field, the Result is

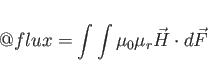
$\begin{displaymath} @flux = \int \int \mu _0 \mu _r \vec{H} \cdot d\vec{F} \end{displaymath}$

-clouds: Analyse Properties of free moving Charges

This Section is for analysing the Results of a Time Domain Computation with free moving Charges.

 ##############################################################################
 # Flags: nomenu, noprompt, nomessage,                                        #
 ##############################################################################
 # Section: -clouds                                                           #
 ##############################################################################
 # symbol  = h_1                                                              #
 # quantity= h                                                                #
 # solution= 1                                                                #
 #                                                                            #
 # position = no              -- 3D Plot of Particle Positions                #
 #   showbox= yes             -- Show computational Box with 3D Plot          #
 # gamma    = yes             -- 2D Plot of Gamma                             #
 # hgamma   = yes             -- 2D Plot of Gamma-density                     #
 #   ihgamma= 30              -- Number of hgamma Bins                        #
 # current  = yes             -- 2D Plot of Q*Velocity                        #
 #  binwidth=  5              -- Bin-Width of Current Average / ChargeSize    #
 #   normal = z               -- Direction of 2D Plots (gamma, current)       #
 # phase    = yes             -- Plots of Velocities vs Position              #
 #   xphase = yes               -- xVelocities vs xPosition                   #
 #   yphase = yes               -- yVelocities vs yPosition                   #
 #   zphase = yes               -- zVelocities vs zPosition                   #
 # export   = no              -- Export raw Cloud Data                        #
 #   outfile= ./gdfidl-exported-clouds                                        #
 ##############################################################################
 # 2dplotopts= -geometry 690x560+10+10                                        #
 #  linecolor= 0              -- 0: foreground, 3: yellow                     #
 #  foreground= black         -- black, white                                 #
 #  background= white         -- blue, white, black                           #
 # showtext     = yes         -- (yes | no)                                   #
 # onlyplotfiles= no          -- (yes | no)                                   #
 ##############################################################################
 # doit, ?, return, end, help, ls                                             #
 ##############################################################################

symbol= QUAN_ISOL:
This is the full Name of the Symbol to be processed. This Field may be a 3D-E-Field or a 3D-H-Field or a Cloud-Dataset.
quantity= QUAN:
This is the first Part of the "symbol".
solution= ISOL:
This is the last Part of the "symbol", the Index of the "symbol".
position= [yes|no]:
Specifies whether a 3d-Plot of the Position of the Clouds shall be produced.
showbox= [yes|no]:
Whether a Box indicating the computational Volume shall be plotted together with the Clouds Positions.
gamma= [yes|no]
Specifies whether a Plot of the relativistic Factor Gamma of the Velocity of the Clouds shall be produced.
hgamma= [yes|no]
Specifies whether a averaging Plot of Gamma shall be produced.
ihgamma= NUMBER
If hgamma= yes, specifies how many Bins of average Gamma shall be used for the hgamma-Plot. The total normal-Extension of the computational Volume will be divided in ihgamma=NUMBER equal Sections.
The Average of the Gamma of all Clouds within the Bins will be plotted.
normal= [x|y|z]
The Normal along which the hgamma Plot will be produced.
phase= [yes|no]
Plots Velocities versus Position.
export= [yes|no]
Writes the full Cloud Data to an ASCII File, whose Name is specified via outfile=WHATEVER.
2dplotopts= ANY STRING CONTAING OPTIONS FOR mymtv2:
gd1.pp does not display the Data itself, but writes a Datafile for mymtv2 (1D and 2D Data) and starts mymtv2 to display these Data.
Useful Options are:
- -geometry X11-GEOMETRY Initial geometry for the X11 window of mymtv2.
showtext= [yes|no]:
This flags, whether the Annotation-Text shall appear in the Plots.
onlyplotfiles= [yes|no]:
This flags, whether Plotfiles shall be written AND mymtv2 or gd1.3dplot shall be started to display them on a X11 Display, or whether only the Plotfiles shall be produced.
doit
The Symbol is loaded from File, the Plotfiles are generated and mymtv2 is started to display the Plotfiles.

-sparameters: Computes scattering Parameters from Time Domain Data

 ##############################################################################
 # Flags: nomenu, noprompt, nomessage,                                        #
 ##############################################################################
 # Section -sparameter                                                        #
 ##############################################################################
 # ports      = all                                                           #
 #               -- (all | LIST )                                             #
 # modes      = ( 1 )                         -- (all | LIST )                #
 # timedata   = no                            -- ( yes | no )                 #
 #   tsumpower= no                            -- ( yes | no )                 #
 #   tintpower= no                            -- ( yes | no )                 #
 #   usample  = 5                             -- Undersample for t-Plots      #
 #   showeh   = yes                           -- show e*h t-Plots             #
 # freqdata   = yes                           -- ( yes | no )                 #
 #   wantdf   = auto                          -- ( auto | REAL )              #
 #   windowed = yes                           -- ( yes | no )                 #
 #     edgeofwindow= 0.70              -- At what Frac. start to apply Window #
 #   fsumpower= yes                           -- ( yes | no )                 #
 #   magnitude= yes                           -- ( yes | no )                 #
 #     slog   = no                            -- ( yes | no )                 #
 #     xlog   = no                            -- ( yes | no )                 #
 #   fintpower= no                            -- ( yes | no )                 #
 #   phase    = no                            -- ( yes | no )                 #
 #   smithplot= no                            -- ( yes | no )                 #
 #     markerat= undefined              -- Want a Marker at .. in Smith-Chart #
 #   groupvelocity= no                        -- ( yes | no )                 #
 #   fri      = no                            -- ( yes | no )                 #
 # excdata    = yes                     -- Show the Data of the Excitation    #
 # upto       = auto                    -- [s]   ( auto | REAL )              #
 # tfirst     = 0.0                     -- [s]                                #
 # flow       = auto                    -- [1/s] ( auto | REAL )              #
 # fhigh      = auto                    -- [1/s] ( auto | REAL )              #
 # ignoreexc  = no                            -- ( yes | no )                 #
 # details    = no                            -- ( yes | no )                 #
 ##############################################################################
 # 2dplotopts= -geometry 690x560+10+10                                        #
 #  linecolor= 0              -- 0: foreground, 3: yellow                     #
 #  foreground= black         -- black, white                                 #
 #  background= white         -- blue, white, black                           #
 # showtext     = yes         -- (yes | no)                                   #
 # onlyplotfiles= no          -- (yes | no)                                   #
 ##############################################################################
 # return, help, end, ls, clearmarkers, doit                                  #
 ##############################################################################

ports:
Possible Values are all, or a List of Names of Ports.
If ports= all, the Time Domain Data of all Ports found in the Database are processed.
If ports is a List of Names, only the Time Domain Data of the Ports whose Names are found in the List are processed.
modes:
Possible Values are all, or a List of Mode-Numbers.
If modes= all, the Time Domain Data of all Modes of the selected Ports found in the Database are processed.
If modes is a List of Mode-Numbers, only the Time Domain Data of the Modes with Numbers in the List are processed.
timedata:
If timedata= yes, the Time Domain Amplitudes of the selected Modes are plotted.
- tsumpower:
  If "yes", the Sum of the Power of the selected Modes is computed as a Function of Time.
- tintpower:
  If "yes", the Sum of the Power of the selected Modes is computed as a Function of Time and integrated over Time.
- usample= NN:
  The undersampling Factor to use for Plots of Time Domain Data.
freqdata:
If freqdata= no, no scattering Parameters are plotted.
- wantdf= DF:
  The wanted Frequency Resolution of the computed scattering Parameters. If wantdf=auto, the computed scattering Parameters have a frequency Resolution of just df = 1 / simulated Time.
  If wantdf=DF , the Time Domain Data are assumed to be Zero outside of the FDTD-simulated time Range. These zero-padded time Signals within a time Range of DT = 1 / DF are FFTed, giving an apparent frequency Resolution of DF.
- windowed:
  If "yes", the Time Domain Data are multiplied by a Window-Function before FFTing them. This damps the Ripples in the scattering Parameters when the Impulse Response is not yet fully computed.
- edgeofwindow= FRAC:
  The Fraction of the simulated Time, where the windowing Function shall start to decay.
  The applied Windowing Function is a Constant '1' from t=0 to FRAC * T, where T is the simulated Time. After FRAC * T, the windowing Function is
  
  $\begin{displaymath}\frac{1}{2} \left[1+\cos(\pi\frac{t-FRAC*T}{(1-FRAC)*T})\right] \end{displaymath}$
- fsumpower:
  If "yes", the Sum of the Power of the selected Modes as a function of Frequency is computed and plotted.
- magnitude:
  If magnitude= yes, the absolute Value of the scattering Parameters are plotted.
- slog:
  If slog= yes, the Magnitude of the scattering Parameters are initially plotted in a logarithmic Plot.
- fintpower:
  If "yes", the Sum of the Power of the selected Modes as a Function of Frequency and integrated over Frequency is computed and plotted.
- phase:
  If phase= yes, the Phase of the scattering Parameters are plotted.
- smithplot:
  If smithplot= yes, the scattering Parameters are plotted in a Smith-Plot.
- markerat= Fi:
  Specifies that you want to have a Marker near the Frequency Fi in the Smith Plots. You may specify an unlimited Number of Frequencies where you want Markers at.
- groupvelocity:
  If groupvelocity= yes, the Groupvelocity is computed from the Phase. The Result is only sensible for Transmissions.
- fri:
  If fri= yes, the scattering Parameters are written in fri-Format to Files.
excdata:
Whether the Data of the Excitation shall be plotted.
upto:
Possible Values are auto or a Time-Value.
If upto= auto, the Time Data up to the last found simulated Time are considered for the Fourier-Transforms.
If upto= TMAX, only the Time-Data upto the Time-Value TMAX are considered for the Fourier-Transforms. This is useful, for the Case that a late Time Instability of the Time Domain Computation has occured, and you want to know the scattering Parameters of a shorter Simulation. THIS SHOULD NOT HAPPEN. IF YOU ENCOUNTER A LATE TIME INSTABILITY, PLEASE SEND THE INPUTFILE WHERE THIS INSTABILITY HAS OCCURED TO "bruns@gdfidl.de".
--
If "upto" is specified as a Value larger than the Time simulated by the FDTD-solver, then the Time Values up to "upto" are filled up with Zeros. This has the Effect that additional Frequency points are computed by FFTing the padded Data Set. The scattering Parameters at the additional Frequency Points are interpolated from the primary Frequency dependent Values by a sin(x)/x Interpolation. For such a Purpose, you should better specify wantdf= DF.
tfirst= TFIRST:
The Time Data lower than TFIRST are discarded and replaced by Zero.
flow:
If flow= auto, the lower Limit of the Frequency Range of the Plots is derived from the Centerfrequency and the Bandwidth of the Excitation as they were specified in the Input for gd1. If flow= FMIN, the lower Limit of the Frequency Range is FMIN.
fhigh:
If fhigh= auto, the upper Limit of the Frequency Range of the Plots is derived from the Centerfrequency and the Bandwidth of the Excitation as they were specified in the Input for gd1. If fhigh= FMAX, the upper Limit of the Frequency Range is FMAX.
ignoreexc:
If ignoreexc= yes, the Spectrum of the excited Mode is ignored. Instead, a flat Spectrum is assumed. This is useful e.g. to compute the Coupling from an relativistic Charge to the Port-Modes.
details:
If yes, a lot of intermediate Data are plotted.
2dplotopts= ANY STRING CONTAING OPTIONS FOR mymtv2:
gd1.pp does not display the Data itself, but writes a Datafile for mymtv2 (1D and 2D Data) and starts mymtv2 to display these Data.
Useful Options are:
- -geometry X11-GEOMETRY Initial geometry for the X11 window of mymtv2.
plotopts= ANY STRING CONTAING OPTIONS FOR gd1-3dplot:
gd1.pp does not display the Data itself, but writes a Datafile for gd1.3dplot (3D Data) and starts gd1.3dplot to display these Data.
Useful Options are:
- -geometry X11-GEOMETRY Initial geometry for the X11 window of gd1.3dplot.
showtext= [yes|no]:
This flags, whether the Annotation-Text shall appear in the Plots.
onlyplotfiles= [yes|no]:
This flags, whether Plotfiles shall be written AND mymtv2 or gd1.3dplot shall be started to display them on a X11 Display, or whether only the Plotfiles shall be produced.
doit:
The scattering Parameters are computed from the Time Domain Amplitudes of the Port-Modes.
clearmarkers:
If you say clearmarkers, the List of Markers which were requested via markerat is cleared.

Example To Compute and Plot the scattering Parameters of only the first two Modes of the Ports with Names Input, Output, we say:

 -sparameter
     modes= ( 1, 2 )
     ports= ( Input, Output )
  doit

Example In the first Step, we compute the Time Domain Amplitudes with gd1:

 gd1 < /usr/local/gd1/examples-from-the-manual/arndt.MTT90.p1854.fig5.gdf

 # /usr/local/gd1/examples-from-the-manual/arndt.MTT90.p1854.fig5.gdf

define(INF,10000.0)
define(MAG, 2) define(PEL, 1) define(CU, 3) define(PER,0)

define(FREQ,15e9)

define(WGH, 15.8e-3)
define(WGW0, 7.9e-3)
define(T0, 6.6e-3)

define(CSW1, 4.2e-3)
define(T1, 6.2e-3)

define(STPSZE, 0.5e-3 )
define(XHIGH, 30e-3) define(XLOW, -XHIGH )
define(ZHIGH, 12e-3) define(ZLOW, -ZHIGH )

########
########
########
 -general
   outfile= /tmp/UserName/arndt
   scratch= /tmp/UserName/arndt-scratch-

 -mesh
   spacing= STPSZE
#   graded= on, qfgraded= 1.2, dmaxgraded= 3e8/FREQ/20
   pxlow= XLOW, pxhigh= XHIGH
   pylow= -WGH/2-STPSZE, pyhigh= 0   # Weg damit
   pylow= 0, pyhigh= WGH/2+STPSZE
   pzlow= ZLOW, pzhigh= ZHIGH
   cxlow= el, cxhigh= el
   cylow= el, cyhigh= mag   # Weg damit
   cylow= mag, cyhigh= ele
   czlow= el, czhigh= mag

 -material
   material= PEL, type= electric
   material= CU,  type= electric

#
# Fill the Universe with Material CU.
#
-brick
   material= CU,
   volume= ( -INF, INF, \
             -INF, INF, \
             -INF, INF)
   doit
#
# The upper and lower Waveguide.
#
   material= 0,
   volume= ( -INF,INF, -WGH/2,WGH/2, T0/2,T0/2+WGW0 ), doit
   vol (-INF,INF, -WGH/2,WGH/2, -(T0/2+WGW0),-T0/2 ), doit

#
# The coupling Slits.
#
   vol ( -CSW1/2,CSW1/2, -WGH/2,WGH/2, -(T0/2+WGW0),T0/2+WGW0 ), doit
   vol ( -(4.2e-3/2+3.0e-3),\
          (4.2e-3/2+3.0e-3),\
          -WGH/2,WGH/2,\
          T0/2,T0/2+WGW0 ),
   doit

   vol ( -(4.2e-3/2+3.0e-3),4.2e-3/2+3.0e-3, -WGH/2,WGH/2, -(T0/2+WGW0),-T0/2 ), do
define(XDUM, 4.2e-3/2+3.0e-3 )
   vol ( -(XDUM+3.2e-3),-XDUM, -WGH/2,WGH/2, -(T0/2+WGW0),T0/2+WGW0 ), do
   vol ( XDUM,XDUM+3.2e-3, -WGH/2,WGH/2, -(T0/2+WGW0),T0/2+WGW0 ), do

define(XDUM, 4.2e-3/2+3.0e-3+3.2e-3+4.2e-3 )
   vol ( -(XDUM+1.6e-3),-XDUM, -WGH/2,WGH/2, -(T0/2+WGW0),T0/2+WGW0 ), do
   vol ( XDUM,XDUM+1.6e-3, -WGH/2,WGH/2, -(T0/2+WGW0),T0/2+WGW0 ), do

 -volumeplot,
#   eyeposition= ( 1.0, 2.0, 0.5) 
   scale= 4.5
   doit

-fdtd
  -ports
     name= xlow1,  plane= xlow,  pzlow = 0, modes= 1, doit
     name= xlow2,  plane= xlow,  pzhigh= 0, modes= 1, doit
     name= xhigh1, plane= xhigh, pzlow = 0, modes= 1, doit
     name= xhigh2, plane= xhigh, pzhigh= 0, modes= 1, doit

  -pexcitation
     port= xlow1,
     mode= 1, amplitude= 1, frequency= 15e9, bandwidth= 10e9,

  -time
     tmin=    100/FREQ
     tmax=  10000/FREQ
     firsts= 10/FREQ
     lasts = 11/FREQ
     distancesave= 0.10/FREQ
     amptresh= 1e-3

  -fdtd
     doit

In the next Step, we start gd1.pp to compute the scattering Parameters from the Time Domain Amplitudes, that were computed by gd1. The Input we give to gd1.pp is:

 -gen, inf @last
 -3da, sy e_1, scal 4.5, arr 5000, fonmat yes, doit
 -spa, window yes, doit
       window no, doit

The resulting Plots are shown in the Figures 2.3 to 2.13.

**Figure 2.3:** The Time Domain electric Field at an early Time.
$\begin{figure}\epsfig{figure=arndt.MTT90.p1854.fig5.ps,width=18cm,bbllx=0pt,bblly=0pt,bburx=747pt,bbury=554pt,clip=}\end{figure}$

**Figure 2.4:** The computed Reflection when a Window has been applied.
$\begin{figure}\epsfig{figure=arndt-res-window-xlow1_out_1-freq-abs.ps,width=15cm,bbllx=0pt,bblly=43pt,bburx=776pt,bbury=575pt,clip=}\end{figure}$

**Figure 2.5:** A computed Transmission when a Window has been applied.
$\begin{figure}\epsfig{figure=arndt-res-window-xlow2_out_1-freq-abs.ps,width=15cm,bbllx=0pt,bblly=43pt,bburx=776pt,bbury=575pt,clip=}\end{figure}$

**Figure 2.6:** A computed Transmission when a Window has been applied.
$\begin{figure}\epsfig{figure=arndt-res-window-xhigh1_out_1-freq-abs.ps,width=15cm,bbllx=0pt,bblly=43pt,bburx=776pt,bbury=575pt,clip=}\end{figure}$

**Figure 2.7:** A computed Transmission when a Window has been applied.
$\begin{figure}\epsfig{figure=arndt-res-window-xhigh2_out_1-freq-abs.ps,width=15cm,bbllx=0pt,bblly=43pt,bburx=776pt,bbury=575pt,clip=}\end{figure}$

**Figure 2.8:** The computed Reflection when no Window has been applied.
$\begin{figure}\epsfig{figure=arndt-res-nowindow-xlow1_out_1-freq-abs.ps,width=15cm,bbllx=0pt,bblly=43pt,bburx=776pt,bbury=575pt,clip=}\end{figure}$

**Figure 2.9:** A computed Transmission when no Window has been applied.
$\begin{figure}\epsfig{figure=arndt-res-nowindow-xlow2_out_1-freq-abs.ps,width=15cm,bbllx=0pt,bblly=43pt,bburx=776pt,bbury=575pt,clip=}\end{figure}$

**Figure 2.10:** A computed Transmission when no Window has been applied.
$\begin{figure}\epsfig{figure=arndt-res-nowindow-xhigh1_out_1-freq-abs.ps,width=15cm,bbllx=0pt,bblly=43pt,bburx=776pt,bbury=575pt,clip=}\end{figure}$

**Figure 2.11:** A computed Transmission when no Window has been applied.
$\begin{figure}\epsfig{figure=arndt-res-nowindow-xhigh2_out_1-freq-abs.ps,width=15cm,bbllx=0pt,bblly=43pt,bburx=776pt,bbury=575pt,clip=}\end{figure}$

**Figure 2.12:** The Sum of the Squares of the computed scattering Parameters when a Window has been applied.
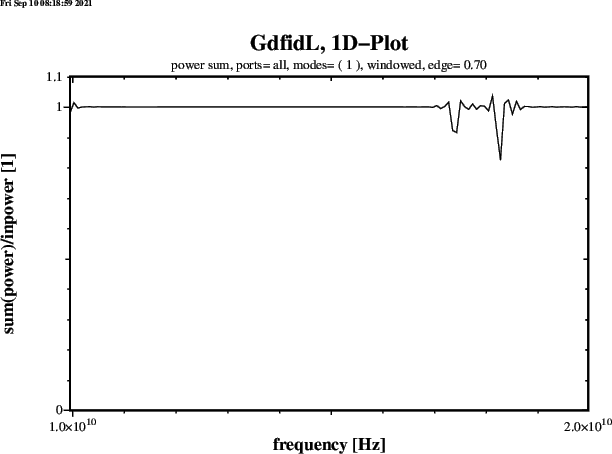$\begin{figure}\epsfig{figure=arndt-res-window-sum-power-freq.ps,width=15cm,bbllx=0pt,bblly=43pt,bburx=776pt,bbury=575pt,clip=}\end{figure}$

**Figure 2.13:** The Sum of the Squares of the computed scattering Parameters when no Window has been applied.
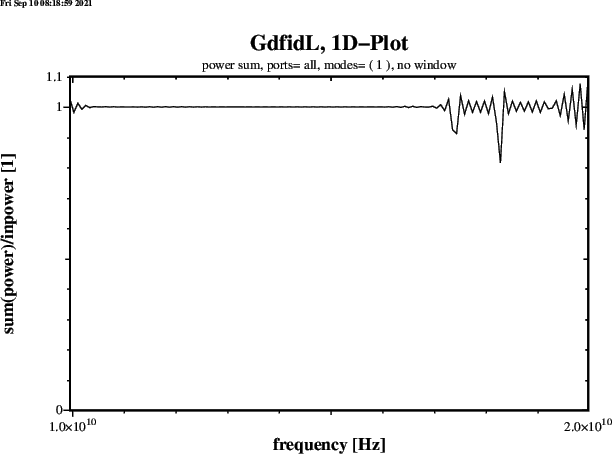$\begin{figure}\epsfig{figure=arndt-res-nowindow-sum-power-freq.ps,width=15cm,bbllx=0pt,bblly=43pt,bburx=776pt,bbury=575pt,clip=}\end{figure}$

Example This Example demonstrates the Usage of tfirst. A Computation with a relativistic Line Charge is performed. The Device is a Button-Beam-Position-Monitor. Only a Quarter of the Device is modeled. There are three Ports where Energy can flow away from the Button. The TEM-Line which is connected to the Button, and the lower and upper Beam-Pipe. The Amplitudes at these Ports is recorded when modes at these Ports is specified larger than Zero.

 gd1 < /usr/local/gd1/examples-from-the-manual/Button-LineCharge.gdf

 # /usr/local/gd1/examples-from-the-manual/Button-LineCharge.gdf

define(INF, 10000)

define(SIGMA, 4.6e-3)
define(STPSZE, 0.15e-3 )

define(A,    40e-3)
define(B,    37e-3)

define(ZYL1, 100e-3)

define(RADO, 3.8e-3)
define(RADI, 3.5e-3)  
define(FEED, 0.33e-3)

define(BUTTON,4.0e-3)
define(CERMA, 4.5e-3)
define(CERME, 6.5e-3)
define(BLOCK, 7.5e-3)

define(EXT, 85e-3)

     
###############################################################

 -general
    outfile= /tmp/UserName/Resultfiles
    scratch= /tmp/UserName/scratch-

 -mesh
    spacing= STPSZE, perfectmesh= no
    graded= yes, dmaxgraded= 4*STPSZE

 define(BUTTONX0, 9.065e-3)
 define(X1, BUTTONX0-RADO)
 define(X2, BUTTONX0+RADO)
 define(NX, 1+(X2-X1)/STPSZE)
    xfixed( NX, X1, X2 )
    zfixed( NX, -RADO, +RADO )

    pxlow= 0, pxhigh= EXT+5e-3
    pylow= 0, pyhigh= 25e-3
    pzlow = -0.01
    pzhigh= +0.01

    cxlow= mag, cxhigh= ele
    cylow= mag, cyhigh= ele
    czlow= el,  czhigh= ele

 #########################################################################
 -material
    material= 3, type= electric
    material= 4, type= electric
    material= 5, type= normal, epsr= 9, muer= 1

-brick
  # Fill the universe with metal..
  material=4 
     volume= (-INF,INF, -INF,INF, -INF,INF)
  doit
 ################################################################
 #vacuum chamber

 -ggcylinder
     material= 0
     originprime= ( 0, 0, 0 )
     xprimedirection= ( 1, 0, 0 )
     yprimedirection= ( 0, 1, 0 )
     range= (-ZYL1/2, ZYL1/2)
 show= later
     clear
       point= ( -36e-3,      -5e-3)
       point= ( -36e-3,       5e-3)
       point= (-20.415e-3,   14e-3)             
       point= ( 20.415e-3,   14e-3)
       point= (  36e-3,       5e-3)
       point= (  56e-3,       5e-3)
       point= (  56e-3,      14e-3)
       point= ( EXT,         14e-3) 
       point= ( EXT,        -14e-3) 
       point= (  56e-3,     -14e-3)
       point= (  56e-3,      -5e-3)
       point= (  36e-3,      -5e-3)
       point= ( 20.415e-3,  -14e-3)
       point= (-20.415e-3,  -14e-3)    
       point= ( -36e-3,      -5e-3)
     doit


 #
 # All four Buttons are modelled, although
 # only one of them is inside the selected Quarter.
 #
 do i= -1, 1, 2
    do j= -1, 1, 2

       #The vacuum part containing the bpm's
       -gbor
           material= 0
           originprime= ( j * BUTTONX0, 14e-3*i, 0 )
           zprimedirection= ( 0, i, 0 )
           rprimedirection= ( 1, 0, 0 )
           range= (0, 360)
 show= later
           clear
              point= (0,       0.)
              point= (0,       4.25e-3)
              point= (27e-3,   4.25e-3)
              point= (27e-3,   0.)
           doit


       # the bpm's
       #the outside shell _1

        material= 3
           clear
              point= (0,        RADO)
              point= (0,        4.25e-3)
              point= (17.5e-3,  4.25e-3)
              point= (17.5e-3,  4.25e-3)
              point= (27e-3,    4.25e-3)
              point= (27e-3,    2.05e-3)
              point= (BLOCK,    2.05e-3) 
              point= (BLOCK,    RADO) 
              point= (0,        RADO)
            doit

       #inner part of the bpm's
            clear
               point= (0,       0.0)
               point= (0,       RADI)
               point= (BUTTON,  RADI)
               point= (BUTTON, 1.65e-3)
               point= (CERMA,  1.65e-3) 
               point= (CERMA,  FEED)  
               point= (CERME,  FEED)  
               point= (CERME,  0.89e-3)  
               point= (27e-3,  0.89e-3)
               point= (27e-3,  0.0e-3)
            doit

       #Al203 part_1
         material= 5
            clear
               point= (CERMA,  FEED)
               point= (CERMA,  RADO)
               point= (CERME,  RADO)
               point= (CERME,  FEED)
            doit
   end do
 end do
###############################################
-volumeplot
      scale=3
      doit
##########################################################################
#
# Wake-Parameters..
#
# For Ports where the Beam passes through, npml=40 or larger is recommended.
#
-fdtd
  -ports
    name= lower_end, plane= zlow,  modes= 10, npml= 40, doit
    name= upper_end, plane= zhigh, modes= 10, npml= 40, doit
    name= bpmho,     plane= yhigh, modes= 1, doit

 -lcharge 
    xpos= 0, ypos= 0,
    charge= 1e-12, sigma= SIGMA
    shigh= 2

 #
 # The Storing of the Fields is just for the nice plot for the Manual.
 #
 -time
    firstsaved= SIGMA / @clight
    lastsaved= (ZYL1 + 20 * SIGMA) / @clight
    distance= SIGMA / @clight

 -fdtd
    doit

The time Data of the Modes at the lower and upper Beam-Pipes are contaminated by the Passing of the Beam through these Ports at small time Values. The Beam has significant Charge ie more than 1e-7 than the Maximum, for times less than $t = 8 \times SIGMA / c$ for the lower Beam Pipe, where it enters. The Beam reaches the upper Beam Pipe after $\Delta t = (z_{max} - z_{min}) / c$ . The Input for gd1.pp to create the following Plots (and some more Plots not shown) is:

 -general,
     infile= @last
     scratch= ./Resultfile-
 -3darrow, sy e_11, arr 1e4, lena 100, fonmat yes, scale 4, doit
 -spa,
       freqdata= no, timedata= yes, tintpower= yes, modes= all

    ports= ( lower_end )
       tfirst= 0, doit
       tfirst= 8 * SIGMA / 3e8, doit
    ports= ( upper_end )
       tfirst= 0, doit
       tfirst= ( @zmax - @zmin + 8 * SIGMA ) / 3e8, doit
    ports= ( bpmho )
       tfirst= 0, doit

**Figure 2.14:** The Time Domain electric Field at an early Time.
$\begin{figure}\epsfig{figure=Button-LineCharge.ps,width=18cm,bbllx=0pt,bblly=0pt,bburx=747pt,bbury=554pt,clip=}\end{figure}$

**Figure 2.15:** The computed Amplitude of the sixth Mode at the lower Beam-Pipe.
$\begin{figure}\epsfig{figure=Button-LineCharge-tfirst-0-port-lower_end-e_amp_of_... ....ps,width=15cm,bbllx=0pt,bblly=43pt,bburx=776pt,bbury=575pt,clip=}\end{figure}$

**Figure 2.16:** The computed Amplitude of the sixth Mode at the lower Beam-Pipe, the time Data while the Beam passes through the Port is replaced by Zeros.
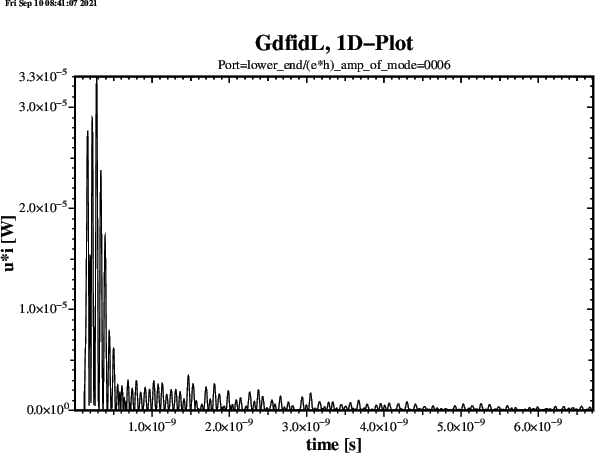$\begin{figure}\epsfig{figure=Button-LineCharge-tfirst-XX-port-lower_end-e_amp_of... ....ps,width=15cm,bbllx=0pt,bblly=43pt,bburx=776pt,bbury=575pt,clip=}\end{figure}$

**Figure 2.17:** The integrated Power of all Modes at the lower Beam-Pipe.
$\begin{figure}\epsfig{figure=Button-LineCharge-tfirst-0-port-lower_end-integral-... ....ps,width=15cm,bbllx=0pt,bblly=43pt,bburx=776pt,bbury=575pt,clip=}\end{figure}$

**Figure 2.18:** The integrated Power of all Modes at the lower Beam-Pipe, the time Data while the Beam passes through the Port is replaced by Zeros.
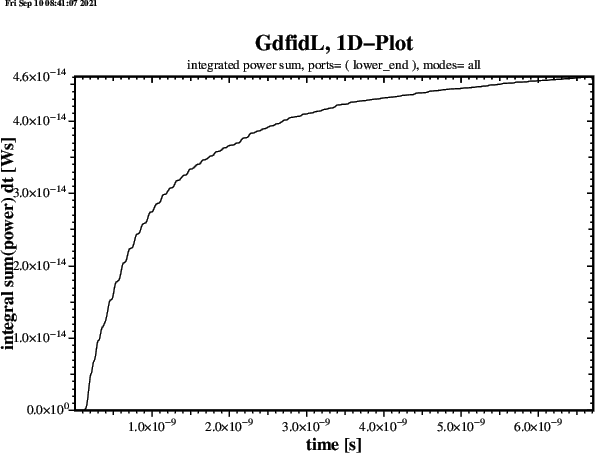$\begin{figure}\epsfig{figure=Button-LineCharge-tfirst-XX-port-lower_end-integral... ....ps,width=15cm,bbllx=0pt,bblly=43pt,bburx=776pt,bbury=575pt,clip=}\end{figure}$

**Figure 2.19:** The computed Amplitude of the sixth Mode at the upper Beam-Pipe.
$\begin{figure}\epsfig{figure=Button-LineCharge-tfirst-0-port-upper_end-e_amp_of_... ....ps,width=15cm,bbllx=0pt,bblly=43pt,bburx=776pt,bbury=575pt,clip=}\end{figure}$

**Figure 2.20:** The computed Amplitude of the sixth Mode at the upper Beam-Pipe, the time Data while the Beam passes through the Port is replaced by Zeros.
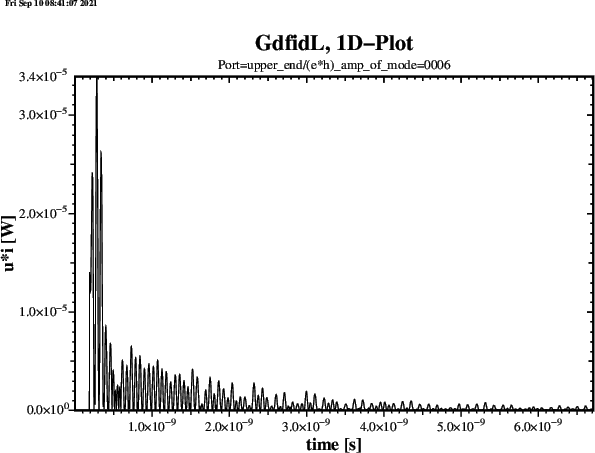$\begin{figure}\epsfig{figure=Button-LineCharge-tfirst-XX-port-upper_end-e_amp_of... ....ps,width=15cm,bbllx=0pt,bblly=43pt,bburx=776pt,bbury=575pt,clip=}\end{figure}$

**Figure 2.21:** The integrated Power of all Modes at the lower Beam-Pipe.
$\begin{figure}\epsfig{figure=Button-LineCharge-tfirst-0-port-upper_end-integral-... ....ps,width=15cm,bbllx=0pt,bblly=43pt,bburx=776pt,bbury=575pt,clip=}\end{figure}$

**Figure 2.22:** The integrated Power of the all Modes at the upper Beam-Pipe, the time Data while the Beam passes through the Port is replaced by Zeros.
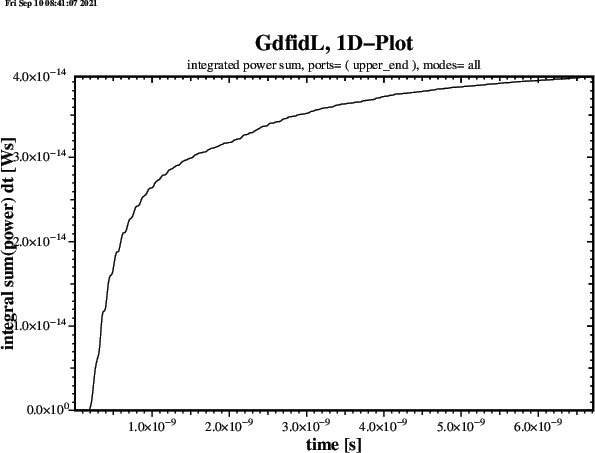$\begin{figure}\epsfig{figure=Button-LineCharge-tfirst-XX-port-upper_end-integral... ....ps,width=15cm,bbllx=0pt,bblly=43pt,bburx=776pt,bbury=575pt,clip=}\end{figure}$

**Figure 2.23:** The integrated Power of all Modes at the BeamPositionMonitor-Port.
$\begin{figure}\epsfig{figure=Button-LineCharge-tfirst-0-port-bpmho-integral-sum-... ....ps,width=15cm,bbllx=0pt,bblly=43pt,bburx=776pt,bbury=575pt,clip=}\end{figure}$

-combine: Combines E- and H-Field to Poynting Field

Help for section "-pcombine": A Poynting-Field is created by combining an E-Field and a H-Field.
The real-Part of the Poyting Field

    Re(S)= a1*Re(E)*Re(H) - b1*Im(E)*Im(H)

The imaginary-Part

    Im(S)= a2*Re(E)*Im(H) + b2*Im(E)*Re(H)

 ##############################################################################
 # Flags: nomenu, noprompt, nomessage,                                        #
 ##############################################################################
 # Section: -pcombine                                                         #
 ##############################################################################
 # Re(S): a1*Re(E)*Re(H) - b1*Im(E)*Im(H)                                     #
 # Im(S): a2*Re(E)*Im(H) + b2*Im(E)*Re(H)                                     #
 #----------------------------------------------------------------------------#
 # a1=        0.50                                                            #
 # a2=        0.50                                                            #
 # b1=        0.50                                                            #
 # b2=        0.50                                                            #
 # eresymbol    = ere_1                                                       #
 #   erequantity= ere                                                         #
 #   eresolution= 1                                                           #
 # eimsymbol    = ere_1                                                       #
 #   eimquantity= ere                                                         #
 #   eimsolution= 1                                                           #
 # hresymbol    = hre_1                                                       #
 #   hrequantity= hre                                                         #
 #   hresolution= 1                                                           #
 # himsymbol    = hre_1                                                       #
 #   himquantity= hre                                                         #
 #   himsolution= 1                                                           #
 # sresymbol    = sre_1                                                       #
 #   srequantity= sre                                                         #
 #   sresolution= 1                                                           #
 # simsymbol    = sim_1                                                       #
 #   simquantity= sim                                                         #
 #   simsolution= 1                                                           #
 ##############################################################################
 # doit, ?, return, end, ls                                                   #
 ##############################################################################

When both a1 and a2 are specified as zero, eresymbol is not referenced and so does not need to be specified.
When both b1 and a2 are specified as zero, himsymbol is not referenced and so does not need to be specfied.
When both b1 and b2 are specified as zero, eimsymbol is not referenced and so does not need to be specfied.
When both a1 and b2 are specified as zero, hresymbol is not referenced and so does not need to be specified.

a1, b1, a2, b2
The Factors by which the E-Field and H- Field is multiplied.
eresymbol, eimsymbol
The Names of the real and imaginary Part of the E-Field.
hresymbol, himsymbol
The Names of the real and imaginary Part of the H-Field.
erequantity, eimquantity, hrequantity, himquantity
The First Part of the Names of the E- andf H-Field.
eresolution, eimsolution, hresolution, himsolution
The Indices of the Fields.
sresymbol, simsymbol:
The Names as which the real and imaginary Part of the Poynting Field shall be stored.
srequantity, simquantity
The first Part of the Name of the Poynting Field.
sresolution, simsolution:
The Indices of the Poynting-Field.
doit:
The relevant E- and H-Fields are fetched from the Database, combined to give a Poynting Field and the reslting Poynting-Field is put into the Database. specified "outfile".

Example In the first Step, we compute the Time Domain Data with gd1:

 gd1 < /usr/local/gd1/examples-from-the-manual/arndt.MTT90.p1854.fig5.gdf

 # /usr/local/gd1/examples-from-the-manual/arndt.MTT90.p1854.fig5.gdf

define(INF,10000.0)
define(MAG, 2) define(PEL, 1) define(CU, 3) define(PER,0)

define(FREQ,15e9)

define(WGH, 15.8e-3)
define(WGW0, 7.9e-3)
define(T0, 6.6e-3)

define(CSW1, 4.2e-3)
define(T1, 6.2e-3)

define(STPSZE, 0.5e-3 )
define(XHIGH, 30e-3) define(XLOW, -XHIGH )
define(ZHIGH, 12e-3) define(ZLOW, -ZHIGH )

########
########
########
 -general
   outfile= /tmp/UserName/arndt
   scratch= /tmp/UserName/arndt-scratch-

 -mesh
   spacing= STPSZE
#   graded= on, qfgraded= 1.2, dmaxgraded= 3e8/FREQ/20
   pxlow= XLOW, pxhigh= XHIGH
   pylow= -WGH/2-STPSZE, pyhigh= 0   # Weg damit
   pylow= 0, pyhigh= WGH/2+STPSZE
   pzlow= ZLOW, pzhigh= ZHIGH
   cxlow= el, cxhigh= el
   cylow= el, cyhigh= mag   # Weg damit
   cylow= mag, cyhigh= ele
   czlow= el, czhigh= mag

 -material
   material= PEL, type= electric
   material= CU,  type= electric

#
# Fill the Universe with Material CU.
#
-brick
   material= CU,
   volume= ( -INF, INF, \
             -INF, INF, \
             -INF, INF)
   doit
#
# The upper and lower Waveguide.
#
   material= 0,
   volume= ( -INF,INF, -WGH/2,WGH/2, T0/2,T0/2+WGW0 ), doit
   vol (-INF,INF, -WGH/2,WGH/2, -(T0/2+WGW0),-T0/2 ), doit

#
# The coupling Slits.
#
   vol ( -CSW1/2,CSW1/2, -WGH/2,WGH/2, -(T0/2+WGW0),T0/2+WGW0 ), doit
   vol ( -(4.2e-3/2+3.0e-3),\
          (4.2e-3/2+3.0e-3),\
          -WGH/2,WGH/2,\
          T0/2,T0/2+WGW0 ),
   doit

   vol ( -(4.2e-3/2+3.0e-3),4.2e-3/2+3.0e-3, -WGH/2,WGH/2, -(T0/2+WGW0),-T0/2 ), do
define(XDUM, 4.2e-3/2+3.0e-3 )
   vol ( -(XDUM+3.2e-3),-XDUM, -WGH/2,WGH/2, -(T0/2+WGW0),T0/2+WGW0 ), do
   vol ( XDUM,XDUM+3.2e-3, -WGH/2,WGH/2, -(T0/2+WGW0),T0/2+WGW0 ), do

define(XDUM, 4.2e-3/2+3.0e-3+3.2e-3+4.2e-3 )
   vol ( -(XDUM+1.6e-3),-XDUM, -WGH/2,WGH/2, -(T0/2+WGW0),T0/2+WGW0 ), do
   vol ( XDUM,XDUM+1.6e-3, -WGH/2,WGH/2, -(T0/2+WGW0),T0/2+WGW0 ), do

 -volumeplot,
#   eyeposition= ( 1.0, 2.0, 0.5) 
   scale= 4.5
   doit

-fdtd
  -ports
     name= xlow1,  plane= xlow,  pzlow = 0, modes= 1, doit
     name= xlow2,  plane= xlow,  pzhigh= 0, modes= 1, doit
     name= xhigh1, plane= xhigh, pzlow = 0, modes= 1, doit
     name= xhigh2, plane= xhigh, pzhigh= 0, modes= 1, doit

  -pexcitation
     port= xlow1,
     mode= 1, amplitude= 1, frequency= 15e9, bandwidth= 10e9,

  -time
     tmin=    100/FREQ
     tmax=  10000/FREQ
     firsts= 10/FREQ
     lasts = 11/FREQ
     distancesave= 0.10/FREQ
     amptresh= 1e-3

  -fdtd
     doit

In the next Step, we start gd1.pp to combine the first stored E-Field and the first stored H-Field to get the Poynting-Field. We display the resulting Field. The Input we give to gd1.pp is:

 -gen, inf @last
 -pcombine
  # Re(s)= a1 * Re(E) * Re(H) - a2 * Im(E) * Im(H)
    a1= 0.5, b1= 0, a2= 0, b2= 0
    eresymbol= e_1
    hresymbol= h_1
    sresymbol= s_1, doit
 -3da, sy= s_1, doit

The resulting Plot is shown in the Figure 2.24.

**Figure 2.24:** The Time Domain Poynting Field at an early Time.
$\begin{figure}\epsfig{figure=arndt.poynting.ps,width=18cm,bbllx=0pt,bblly=0pt,bburx=747pt,bbury=554pt,clip=}\end{figure}$

-material: Conductivities of electric Materials

This Section allows the Changing of the Conductivities of Materials with type= electric. These Conductivities are used for estimating the Wall Losses in the Section -losses.

 ##############################################################################
 # Flags: nomenu, noprompt, nomessage,                                        #
 ##############################################################################
 # section -material                                                          #
 ##############################################################################
 # material=  1        epsr....: infinity      kappa    =      58.0e+6        #
 # type: electric         xepsr: infinity        xkappa =      58.0e+6        #
 #                        yepsr: infinity        ykappa =      58.0e+6        #
 #                        zepsr: infinity        zkappa =      58.0e+6        #
 #                     muer....:       0.0     mkappa   :       0.0           #
 #                        xmuer:       0.0       xmkappa:       0.0           #
 #                        ymuer:       0.0       ymkappa:       0.0           #
 #                        zmuer:       0.0       zmkappa:       0.0           #
 ##############################################################################
 # return, help, ls                                                           #
 ##############################################################################

material
The Material Index of the Material whose Conductivity is to be changed.
kappa
The electric Conductivity of the Material in MHO/m (1/Ohm/m).
xkappa, ykappa, zkappa
The x-, y-, z-Value of an anisotropic Material. Only diagonal Kappa Matrices can be specified.

In gd1.pp, the Values for type, epsr, muer, mkappa cannot be changed.
Example To specify that Wall Loss Computations in the Section -wlosses shall use a Conductivity of $30 \times 10^6$ for the Material '10', we say:

 -material
    material= 10
    kappa= 30e6

-wakes: longitudinal and transverse Wakepotentials

This Section allows the Computation of longitudinal and transverse Wake Potentials from Data that were computed by gd1. These Data are only recorded by gd1 when you did specify a Charge in the Section -lcharge of gd1.

gd1 computes the Integral of the component along the outermost Paths where a Witness-Particle can travel and stores the Result in the Database. Since from these Data the longitudinal and transverse Wakepotentials everywhere in the Beam Pipe can be computed, you can specify an unlimited Number of Positions (x,y) where you are interested in the Wakepotentials. The (x,y) Position of the exciting Charge cannot be changed afterwards, though.

 ##############################################################################
 # Flags: nomenu, noprompt, nomessage,                                        #
 ##############################################################################
 # section -wakes                                                             #
 ##############################################################################
 # set =     0      -- What Dataset (windowwake only)                         #
 # watq      = yes  -- Process all Wakes at Positions of Line-Charges         #
 # awtatq    = yes  -- Use the Average of the two nearest transverse Wakes    #
 #                  -- as the transverse Wakes at the Positions of Charges    #
 # impedances= no   -- Compute Impedances.                                    #
 #    wantdf = auto           -- Wanted freq Resolution => SIN(f)/f Interpol. #
 #    window = yes            -- Apply Hann-Window when computing Impedances. #
 #     fhigh =  undefined          -- fhigh of Impedances.                    #
 #    excitation= charge           -- {charge|port}.                          #
 # uselu= yes            -- Use Sparse LU-Factorisation (not MG).             #
 #   niter =   2         -- nIter for MG                                      #
 #   omega =    1.10     -- Omega for MG                                      #
 #   Omega2=    1.10     -- Omega2 for MG                                     #
 #   mgdetails= no       -- Show Number of its etc                            #
 # uselowpass= no        -- Use lowpass Filtering.                            #
 # usehighpass= no       -- Use highpass Filtering.                           #
 # showchargemax= no     -- Show Value of Charge Maximum.                     #
 # sbunchspectrum= no    -- Show Spectrum of the Current(, when imp=yes).     #
 # centerbunch= yes      -- Shift Data. Bunch Center will be at s=0.          #
 # peroffset= no         -- Scale Wx by x, Wy by y.                           #
 # xyref   = ( 0.0, 0.0)                        -- refpoint for ??atxy-Data   #
 # usexyref= no                                 -- Use refpoint?              #
 # clear            -- Clears all the "w*at*" Values.                         #
 # watxy = ( undefined, undefined)                  -- want wz(xi,yi,s), i= 1 #
 # wxatxy= ( undefined, undefined)                  -- want wx(xi,yi,s), i= 1 #
 # wyatxy= ( undefined, undefined)                  -- want wy(xi,yi,s), i= 1 #
 # watsi = undefined                  -- want w(x,y,si), i= 1                 #
 # watxi = undefined                  -- want w(xi,y,s), i= 1                 #
 #   liny= 20                         -- Number of Lines in y-Direction.      #
 # watyi = undefined                  -- want w(x,yi,s), i= 1                 #
 #   linx= 20                         -- Number of Lines in x-Direction.      #
 # wxatxi= undefined                  -- want wx(xi,y,s), i= 1                #
 # wxatyi= undefined                  -- want wx(x,yi,s), i= 1                #
 # wyatxi= undefined                  -- want wy(xi,y,s), i= 1                #
 # wyatyi= undefined                  -- want wy(x,yi,s), i= 1                #
 # istrides= 3                        -- Distance of s-Points of the Plots    #
 #                                    --                 in Units of "ds".    #
 # slow =        0.0                  -- Lowest s-Value to consider.          #
 # shigh=  undefined                  -- Highest s-Value to consider.         #
 # watsfiles = -none-
 #   xlowwats =       -1.0e+30                                                #
 #   xhighwats=        1.0e+30                                                #
 #   ylowwats =       -1.0e+30                                                #
 #   yhighwats=        1.0e+30                                                #
 # frequency=  undefined ( @ufrequency :  undefined )                         #
 #   ( @zxesrf:  undefined )                                                  #
 #   ( @zxesrf:  undefined )                                                  #
 #   ( @zxesrf:  undefined )                                                  #
 #  ( @xloss :  undefined ) [VAs]                                             #
 #  ( @yloss :  undefined ) [VAs]                                             #
 #  ( @zloss :  undefined ) [VAs]                                             #
 #  ( @charge:  undefined ) [As]                                              #
 ##############################################################################
 # 2dplotopts= -geometry 690x560+10+10                                        #
 #  linecolor= 0              -- 0: foreground, 3: yellow                     #
 #  foreground= black         -- black, white                                 #
 #  background= white         -- blue, white, black                           #
 # showtext     = yes         -- (yes | no)                                   #
 # onlyplotfiles= no          -- (yes | no)                                   #
 ##############################################################################
 # return, help, end, clear, doit                                             #
 ##############################################################################

set= NUMBER-OF-SET
For Results from -windowwake only. What Dataset to process. When a Computation is performed with -windowwake, one can compute in a single Run the Wakepotentials of different Numbers of periodic Sections of a periodic Geometry. The different Results are call Sets. The Number of the Set to analyse is specified.
watq= yes $\vert$ no
watq stands for "Wake at Q-position". If watq= yes, then the longitudinal and transverse Wakepotentials at the x-y-Position of the exciting Charge are computed. You do not have to specify this Position by yourself.
awtatq= yes $\vert$ no
awtatq stands for "Average Wakes (transverse) at Q-Position". In the Grid, the transverse Wakepotentials are best defined just in between the Grid Planes. But the exciting Charge can only travel along a Grid Line (the crossing Line of two Grid Planes). So the transverse Wakepotential just at the Position of a Charge is not well defined.
If awtatq= yes, gd1.pp computes the transverse Wakepotentials at the two Positions between the Grid Planes that are nearest to the Position of the exciting Charge. The Average of the two Potentials are then assumed to be the transverse Wakepotential at the Position of the Charge.
impedances= yes $\vert$ no
If impedances= yes, the Spectrum of Wakepotentials at Points (x,y) are computed and divided by the Spectrum of the exciting Current.
window= yes $\vert$ no
If yes, a Hann-Window is applied to the Wakepotentials, before they are Fouriertransformed to compute the Impedances.
fhigh= NUMBER
The upper Frequency of the Range to compute the Impedances in. If you do not specify that Parameter, gd1.pp choses a Value such that at that Frequency, sufficient Energy is in the Spectrum of the exciting charge, and that the Grid-Spacing is fine enough to resolve the corresponding Wavelength.
uselu= yes $\vert$ no
Specifies that a LU-Decomposition shall be used to solve the linear Equations. If uselu=no, the linear Equations are solved with an iterative Scheme, which requires less memory, but much more time.
uselowpass= yes $\vert$ no
If yes, the Wakepotentials are lowpass filtered in the s-Domain. The Upper-Frequency of that Filter is about 0.9 times the highest possible Frequency in the Drid.
usehighpass= yes $\vert$ no
If yes, the Wakepotentials are highpass filtered in the s-Domain.
showchargemax= yes $\vert$ no
If yes, at the Maximum of the Charge in the Plots its numeric Value is written to.
centerbunch= yes $\vert$ no
If yes, the s-Coordinate is shifted such that the maximum of the exciting Charge is at s=0.
peroffset= yes $\vert$ no
If yes, the transverse Wakepotentials and Impedances are plotted after scaling by their x- and y-Positions.
xyref= (XREF, YREF)
usexyref= yes $\vert$ no
Specifies whether the transverse Wakepotentials shall be computed with Reference to the Wakepotentials at (XREF, YREF). If usexyref=yes, the transverse Wakepotentials at (XREF,YREF) are computed, and the other transverse Wakepotentials are plotted as eg. .
clear
Clear the List of Positions where to plot Wakepotentials in Addition to the watq's. See the Explanation for watxy, wxatxy, wyatxy, watsi, watxi, watyi, wxatxi, wxatyi, wyatxi, wyatyi below.
watxy= (Xi, Yi), wxatxy= (Xi, Yi), wyatxy= (Xi, Yi)
watxy, wxatxy, wyatxy stands for "Wake at xy-Position, Wake in x at xy-Position, Wake in y at xy-Position". If you specify watxy= (Xi, Yi), the longitudinal Wakepotential at the Gridpoint nearest to the specified Position (Xi, Yi) will be computed. Similiar, when you specify wxatxy= (Xi, Yi) or wyatxy= (Xi, Yi), the transverse Wakepotentials at the Midpoints between Gridpoints nearest to the specified Position (Xi, Yi) will be computed.
You can specify an unlimited Number of (x,y)-Positions where you want to know the longitudinal or transverse Wakepotentials.
watsi= Si
watsi stands for "Wake at S-Position". If you specify watsi= Si, the longitudinal Wakepotential in the whole (x,y) Region of the Beam Pipe at the s-Value Si will be computed and plotted.
You can specify an unlimited Number of s-Positions where you want to have such Plot.
watxi= Xi, watyi= Yi watxi stands for "Wake at x-Position", watyi stands for "Wake at y-Position", If you specify watxi= Xi or watyi= Yi, the longitudinal Wakepotential at the Position Xi, or Yi will be plotted as a Function of (y,s) or (x,s), respectively. These Functions will be plotted with liny or linx Lines respectively.
You can specify an unlimited Number of y- or y-Positions where you want to know the longitudinal Wakepotentials.
linx= LX, liny= LY
Number of Lines to use to Plot the Data requested with watxi= Xi, watyi= Yi.
wxatxi= Xi, wxatyi= Yi, wyatxi= Xi, wyatyi= Yi
wxatxi, wxatyi, wyatxi, wyatyi stands for "Wake in x at x-Position, Wake in x at y-Position, Wake in y at x-Position, Wake in y at y-Position".
If you specify wxatxi= Xi, the transverse Wakepotential in x-Direction will be plotted in the y-s Plane at the x-Coordinate between Meshplanes nearest to Xi.
If you specify wxatyi= Yi, the transverse Wakepotential in x-Direction will be plotted in the x-s Plane at the y-Coordinate between Meshplanes nearest to Yi.
If you specify wyatxi= Xi, the transverse Wakepotential in y-Direction will be plotted in the y-s Plane at the x-Coordinate between Meshplanes nearest to Xi.
If you specify wyatyi= Yi, the transverse Wakepotential in y-Direction will be plotted in the x-s Plane at the y-Coordinate between Meshplanes nearest to Yi.
You can specify an unlimited Number of y- or y-Positions where you want to know the transverse Wakepotentials.
istrides= IS
Specifies the Distance of s-Values in the Plots requested via watxy, wxatxy, wyatxy, watsi, watxi, watyi, wxatxi, wxatyi, wyatxi, wyatyi. These Plots contain a huge Amount of Data when large s-Values are present. It may happen that mymtv2 needs a long Time to load these Datasets, and also there may be way too much s-Values in the Plots. With a Value greater than 1 of this Parameter you can reduce the Information in these Plots.
slow= SLOW
The lowest s-Value to consider for the w?at??-Plots.
shigh= SHIGH
The highest s-Value to consider for everything.
watsfiles=
If specified, the raw Data of the Wakepotentials in the x-y-Plane is written to ascii files. The Format is self-explanatory.
xlowwats etc the limiting Planes of the Region where w(x,y,s) shall be written to wats-Files.
frequency
A special Parameter for Dr Guenzel. All others: Ignore it.
2dplotopts= ANY STRING CONTAING OPTIONS FOR mymtv2:
gd1.pp does not display the Data itself, but writes a Datafile for mymtv2 (1D and 2D Data) and starts mymtv2 to display these Data.
Useful Options are:
- -geometry X11-GEOMETRY Initial geometry for the X11 window of mymtv2.
plotopts= ANY STRING CONTAING OPTIONS FOR gd1-3dplot:
gd1.pp does not display the Data itself, but writes a Datafile for gd1.3dplot (3D Data) and starts gd1.3dplot to display these Data.
Useful Options are:
- -geometry X11-GEOMETRY Initial geometry for the X11 window of gd1.3dplot.
showtext= [yes|no]:
This flags, whether the Annotation-Text shall appear in the Plots.
onlyplotfiles= [yes|no]:
This flags, whether Plotfiles shall be written AND mymtv2 or gd1.3dplot shall be started to display them on a X11 Display, or whether only the Plotfiles shall be produced.
doit
The requested Wakepotentials are computed from the Data in the Database, for each Dataset an Instance of mymtv2 is started to plot the Data.

Note: The longitudinal and transverse Lossfactors are printed in the Plots. They are also available as the Symbols @zloss, @xloss, @yloss after a Wakepotential Computation.
Example To have plotted the longitudinal Wakepotential at the Planes x=1e-3 and x=2e-3:

 -wake
    watxi= 1e-3
    watxi= 2e-3

-totouchstone: Convert fri-data to TouchStone Format

This Section allows the Combination of scattering Parameters in fri-Files to TouchStone Files.
The Section -sparameter may be used to generate the fri-Files.

 ##############################################################################
 # Flags: nomenu, noprompt, nomessage,                                        #
 ##############################################################################
 # section: -totouchstone                                                     #
 ##############################################################################
 # outfile= ./s-matrix.sXp                                                    #
 # ports= 2                                                                   #
 # normalise= no                                                              #
 #                                                                            #
 # ij= (1,1)                  -- Index of S-Parameter.                        #
 # file=  -none-
 #                            -- Filename of S-Parameter.                     #
 # factor= 1.0                -- Factor to apply.                             #
 # iport=  1, fcutoff= 0.0                                                    #
 # ###                                                                        #
 # Already specified Files:                                                   #
 # ij: (1,1), factor: 1.0, fcutoff: 0.0                                       #
 #   file:  -none-
 # ij: (1,2), factor: 1.0, fcutoff: 0.0                                       #
 #   file:  -none-
 # ij: (2,1), factor: 1.0, fcutoff: 0.0                                       #
 #   file:  -none-
 # ij: (2,2), factor: 1.0, fcutoff: 0.0                                       #
 #   file:  -none-
 ##############################################################################
 # clear, doit, ?, return, end, help, ls                                      #
 ##############################################################################

outfile= VALID-FILENAME:
The Name of the RouchStone-File to be generated. If the File exists, it will be overwritten.
ports= NN:
The Order of the scattering Matrix to write to the TouchStone File. If the Order is N, N*N scattering Parameters have to be specified as fri-Files.
normalise:
If yes, the scattering Matrices will be normalised such that each Column is a Unit Vector.
ij= (I, J):
The Indices of the scattering Parameter to be specified as a fri-File.
file= NAME-OF-A-FRI-FILE:
The Name of the fri-File which contains the Data of the scattering Parameter with Indices (I, J).
factor= NUMBER:
The Data in the fri-File will be multiplied by NUMBER before it is written to the TouchStone-file.
doit
The scattering Parameters are read from the specified Files and are written to the TouchStone-File.

Note: All fri-Files must have the same frequency Resolution (use wantdf= DF), and must have the same frequency Range.
Example The following Shell-Script computes the four Rows of the scattering Matrix of a four-Port Device, by exciting four times a different Port. The computed scattering Parameters are stored as fri-Files and are combined to one TouchStone-File.

#!/bin/sh

#
# First Step:
# Computation of the four rows of the scattering matrix.
# The results of each computation are stored in a different file.
#
#    In the inputfile "arndt.00.x.gdf", the outfile is defined as
#       outfile= /tmp/bruw1931/garbage/arndt-excitation-at-PEXC
#
#
# At each computation, a different port is excited.
#
#    In the inputfile, the excitation is defined via:
#  -pexcitation
#     port= PEXC,
#     mode= 1, amplitude= 1, frequency= 17e9, bandwidth= 20e9,
#

 for PEXC in xlow1 xhigh1 xlow2 xhigh2
 do
    gd1 -DPEXC=$PEXC < arndt.00.x.gdf | tee out-excitation=$PEXC
 done

#
# Fouriertransform, and generating fri-files.
# The names of the fri-files are defined via
#
#  -general, scratch= /tmp/bruw1931/garbage/exc-at-$PEXC-
#
# Frequency resolution is 10 MHz  (wantdf= 10e6)
#
 for PEXC in xlow1 xhigh1 xlow2 xhigh2
 do
    gd1.pp << EOF
      -general
         infile= /tmp/bruw1931/garbage/arndt-excitation-at-$PEXC
         scratch= /tmp/bruw1931/garbage/exc-at-$PEXC-
      -sparameter
         window= yes, edgeofwindow= 0.7
         wantdf= 10e6
         flow= 5e9, fhigh= 25e9
         timedata= no, fsumpower= no, magnitude= no, phase= no, smithplot= no
         fri= yes
         onlyplotfiles= yes
         doit
EOF
 done

#
# Second step.
# Combining the rows of the scattering matrix to one TouchStone-file.
#

 gd1.pp << EOF
 -totouchstone
    clear     # file= - undefined -
    ports= 4

 sdefine(BASE, /tmp/bruw1931/garbage/exc-at)
    sdefine(P1, xlow1) sdefine(P2, xhigh1)
    sdefine(P3, xlow2) sdefine(P4, xhigh2)
      ij= (1,1), file= [BASE]-[P1]-[P1]_out_1.fri
      ij= (1,2), file= [BASE]-[P1]-[P2]_out_1.fri
      ij= (1,3), file= [BASE]-[P1]-[P3]_out_1.fri
      ij= (1,4), file= [BASE]-[P1]-[P4]_out_1.fri

      ij= (2,1), file= [BASE]-[P2]-[P1]_out_1.fri
      ij= (2,2), file= [BASE]-[P2]-[P2]_out_1.fri
      ij= (2,3), file= [BASE]-[P2]-[P3]_out_1.fri
      ij= (2,4), file= [BASE]-[P2]-[P4]_out_1.fri

      ij= (3,1), file= [BASE]-[P3]-[P1]_out_1.fri
      ij= (3,2), file= [BASE]-[P3]-[P2]_out_1.fri
      ij= (3,3), file= [BASE]-[P3]-[P3]_out_1.fri
      ij= (3,4), file= [BASE]-[P3]-[P4]_out_1.fri

      ij= (4,1), file= [BASE]-[P4]-[P1]_out_1.fri
      ij= (4,2), file= [BASE]-[P4]-[P2]_out_1.fri
      ij= (4,3), file= [BASE]-[P4]-[P3]_out_1.fri
      ij= (4,4), file= [BASE]-[P4]-[P4]_out_1.fri

     outfile= /tmp/bruw1931/garbage/touchstone.s4p

    doit
EOF

##############

-combine: Build scattering Matrices via scattering other scattering Matrices

This Section allows the Combination of scattering Matrices of several Devices to the resulting scattering Matrix of the combined Device.

 ##############################################################################
 # Flags: nomenu, noprompt, nomessage,                                        #
 ##############################################################################
 # section: -combine                                                          #
 ##############################################################################
 # outfile= ./s-matrix.sXp
 # show= yes                            -- Give a Plot of the resulting       #
 #                                      -- Scattering Parameters.             #
 # kdevice= 1, smatrix=  -none-
 # kdevice= 2, smatrix=  -none-
 # kdevice= 3, smatrix=  -none-
 # p1ik= ( 1, 1 ), p2ik= ( 1, 2 ), factor= 1.0                                #
 #  fcutoff= 0.0, epsmue= 1.0, linelength= 0.0                                #
 # rpi= 1, pik= ( 1, 1 )                                                      #
 # ####                                                                       #
 # Specified Port Connections:                                                #
 #     -- none so far --                                                      #
 # ####                                                                       #
 # Specified outer Ports:                                                     #
 #     -- none so far --                                                      #
 ##############################################################################
 # connect, assign, clear, doit, ?, return, end, help                         #
 ##############################################################################

outfile=
The Name of the File where the resulting scattering Matrix will be written to. The File will be written in TOUCHSTONE-Format.
kdevice= NUMBER, smatrix= FILENAME
The Number of some Device, and the File where its scattering Parameters are to be found in. The smatrix-File has to contain the Data in TouchStone-Format. There can be up to 100 Devices.
p1ik= ( I1, K1 ), p2ik= ( I2, K2 ), factor= FACTOR,
fcutoff= FC, epsmue= EPSMUE, linelength= LL, connect
The Port I1 of device K1 is connected to the Port I2 of Device K2 via a Line of Length=LL. The Line has the Parameters cutoff=FC, eps*mue=EPSMUE. The Damping of the Line is FACTOR.
rpi= IRPI, pik= (I,K), assign
The Port pik(I,K) is declared to be the outer Port IRPI of the resulting Device.
show= [yes|no]:
Give a Plot of the resulting scattering Parameters.
doit:
The resulting scattering Matrix is computed and written to the specified "outfile".

Example

 -combine
  outfile= ./filter.s2p
    kdevice= 1, smatrix= /tmp/UserName/ipart=1.s2p
    kdevice= 2, smatrix= /tmp/UserName/ipart=2.s2p
    kdevice= 3, smatrix= /tmp/UserName/ipart=1.s2p
 
 
   # Connect the Ports at the Cutplanes.
   # i: Port, k: Device
    p1ik = (2,1), p2ik = (1,2), fcutoff= 3.2e9,
         epsmue= 1, linelength= -5e-3, factor= 1, connect
    p1ik = (2,2), p2ik = (2,3), fcutoff= 3.2e9,
         epsmue= 1, linelength= -5e-3, factor= 1, connect
 
   # rpi : Resulting Port I
   # pik : Port I of device K
   rpi= 1, pik= (1,1), assign
      # The port '1' of the resulting device shall be the port '1' of device '1'.
   rpi= 2, pik= (1,3), assign
      # The port '2' of the resulting device shall be the port '1' of device '3'.
 doit

-smonitor: Analyse scalar Time Domain Signals

This Section is for analysing Data monitored via gd1's section -smonitor, ie. scalar Flux Quantities.

 ##############################################################################
 # Flags: nomenu, noprompt, nomessage,                                        #
 ##############################################################################
 # section: -smonitor                                                         #
 ##############################################################################
 # symbol  = - none -                                                         #
 # timedata   = yes                    -- ( yes | no )                        #
 # upto       = auto                   -- [s]   ( auto | REAL )               #
 # freqdata   = yes                    -- ( yes | no )                        #
 #   wantdf   = auto                   -- ( auto | REAL )                     #
 #   windowed = yes                    -- ( yes | no )                        #
 #     edgeofwindow= 0.70              -- At what Frac. start to apply Window #
 #   flow     = auto                   -- [1/s] ( auto | REAL )               #
 #   fhigh    = auto                   -- [1/s] ( auto | REAL )               #
 ##############################################################################
 # 2dplotopts= -geometry 690x560+10+10                                        #
 #  linecolor= 0              -- 0: foreground, 3: yellow                     #
 #  foreground= black         -- black, white                                 #
 #  background= white         -- blue, white, black                           #
 # showtext     = yes         -- (yes | no)                                   #
 # onlyplotfiles= no          -- (yes | no)                                   #
 ##############################################################################
 # doit, ?, return, end, help, ls                                             #
 ##############################################################################

symbol= BLA_BLA_BLUB:
The Name which was specified to monitor the scalar Quantity.
timedata= [yes|no]:
Specifies whether you want to have a Plot of the recorded Time-History of the scalar Quantity.
upto= [auto|REAL]:
Up to what Time the Data shall be analysed.
freqdata= [yes|no]:
Specifies whether you want to get a Plot of the fft'ed Time History.
wantdf= REAL:
The wanted frequency Resolution of the freq-Data.
windowed= [yes|no]:
Specifies whether you want to have a Hann-Window applied to the Time Domain Data before the fft is done.
edgeofwindow= REAL:
Specifies the Fraction where the Decay of the Hann-Window shall start.
flow, fhigh : REAL:
The lower and upper frequency Limit of the freq-Plot.
2dplotopts= ANY STRING CONTAING OPTIONS FOR mymtv2:
gd1.pp does not display the Data itself, but writes a Datafile for mymtv2 (1D and 2D Data) and starts mymtv2 to display these Data.
Useful Options are:
- -geometry X11-GEOMETRY Initial geometry for the X11 window of mymtv2.
plotopts= ANY STRING CONTAING OPTIONS FOR gd1-3dplot:
gd1.pp does not display the Data itself, but writes a Datafile for gd1.3dplot (3D Data) and starts gd1.3dplot to display these Data.
Useful Options are:
- -geometry X11-GEOMETRY Initial geometry for the X11 window of gd1.3dplot.
showtext= [yes|no]:
This flags, whether the Annotation-Text shall appear in the Plots.
onlyplotfiles= [yes|no]:
This flags, whether Plotfiles shall be written AND mymtv2 or gd1.3dplot shall be started to display them on a X11 Display, or whether only the Plotfiles shall be produced.
doit:
The selected Symbol is read from the Database and the Analysis is performed. Plotfiles are generated and mymtv2 is started to display the Plotfiles.

-fexport: Export 3D-Fields to ASCII Files

3D E and H Fields can be exported to ASCII files. Also Portmode Fields can be exported.

 ##############################################################################
 # Flags: nomenu, noprompt, nomessage,                                        #
 ##############################################################################
 # Section: -fexport                                                          #
 ##############################################################################
 # symbol  = h_1                                                              #
 # quantity= h                                                                #
 # solution= 1                                                                #
 #   phase =  45.0000         -- Only for Portmodes.                          #
 # bbxlow  =    -1.0000e+30, bbylow =    -1.0000e+30, bbzlow =    -1.0000e+30 #
 # bbxhigh =     1.0000e+30, bbyhigh=     1.0000e+30, bbzhigh=     1.0000e+30 #
 # outfile = ./gdfidl-exported-field                                          #
 ##############################################################################
 # doit, ?, return, end, help, ls                                             #
 ##############################################################################

symbol= QUAN_ISOL:
This is the full Name of the Symbol to be processed. This Field has may be a 3D-E-Field or a 3D-H-Field or a Portmode Field.
quantity= QUAN:
This is the first Part of the "symbol".
solution= ISOL:
This is the last Part of the "symbol", the Index of the "symbol".
bbxlow=,bbxhigh=,bbylow=bbyhigh=,bbzlow=,bbzhigh=:
Specifies the Limits of a bounding Box. Only the Fields that lie within the Box are written.
outfile=:
The Name of the File to write the Field values to.
doit:
The Exportfile is written. The Format of the File should be self-explanatory.

-2dmanygifs: Create many GIF Files

3D-Fields which were exported via gd1's section -fexport or gd1.pp's Section -fexport can be used to create GIF-Files.

 ##############################################################################
 # Flags: nomenu, noprompt, nomessage,                                        #
 ##############################################################################
 # Section: -2dmanygifs                                                       #
 ##############################################################################
 # 1stinfile = /tmp/UserName/fexported--000000000.gz                          #
 # outfiles  = auto                                                           #
 # mpegfile  = 2dmanygifs.mpeg                                                #
 # uptonfiles= 1000000000                                                     #
 # ixoffset  = 0                                                              #
 # iyoffset  = 0                                                              #
 # stride    = 1                                                              #
 # width     = 1000                                                           #
 # scale     = 1.0                                                            #
 # what      = rHy                      -- rHx,rHy,Hx,Hy,Ezx,Ezy              #
 # log       = no                       -- plot log(1+|scale*f|)              #
 # zerolines = yes                      -- Plot Lines at f=0                  #
 # show      = yes                      -- Show the mpeg.                     #
 ##############################################################################
 # doit, ?, return, end, help                                                 #
 ##############################################################################

1stinfile= FILENAME-NUMBER:
The first File to read.
outfiles:
The Basename of the GIF-Files to be written. If outfiles=auto, the GIF-Files will have the same Name as the read fexported Files, with the Letters .gif attached.
mpegfile:
The Name of the mpeg File to create from the many GIFs.
uptonfiles=NFILES:
How many GIF-Files to create. gd1.pp will try to read the first File, given by 1stinfile=FILENAME, and guess the next Files from the Name of the first File, ie. it will count up the trailing Number. It will read up to NFILES.
ixoffset=IX0, iyoffset= IY0, what= [rHx|rHy]:
The Plots are 2d-Plots of a Field Component in a Plane. The Plane of the 3D-Field in the fexported Files to take is the IX0.th Plane, or the IY0.th Plane.
what=rHx gives Plots of the x-Component of the Field, multiplied by the distance from the Axis, what=rHy gives Plots of the y-Component of the Field, multplied by the Distance from the Axis.
doit:
The Files are read, the GIFs are generated, and it is tried to create a mpegfile from the GIFs.

-3dmanygifs: Create many GIF Files

Datasets of H-Fields on Surfaces exported via gd1's Section -fexport, what=honmat can be used to create GIF-Files.

 ##############################################################################
 # Flags: nomenu, noprompt, nomessage,                                        #
 ##############################################################################
 # Section: -3dmanygifs                                                       #
 ##############################################################################
 # 1stinfile = /tmp/UserName/H-onmat--000000001.gz                            #
 # outfiles  = auto                                                           #
 # uptonfiles= 1000000000                                                     #
 # stride =              1                                                    #
 # what      = abs                      -- abs, logabs, loglogabs             #
 # mpegfile  = ./3dmanygifs.mpeg                                              #
 # eyeposition  = ( undefined, undefined, undefined )                         #
 # rotsequence= xyz                                                           #
 # xrot = -30.0                                                               #
 # yrot = 40.0                                                                #
 # zrot = 0.0                                                                 #
 # dxrot= 0.0                                                                 #
 # dyrot= 0.0                                                                 #
 # dzrot= 0.0                                                                 #
 # scale= 1.0                           -- Plot scale*f.                      #
 # width= 1000                          -- Width of the GIFs.                 #
 # show= yes                            -- Show the mpeg                      #
 ##############################################################################
 # doit, ?, return, end, help                                                 #
 ##############################################################################

1stinfile= FILENAME-NUMBER:
The first File to read.
outfiles:
The Basename of the GIF-Files to be written. If outfiles=auto, the GIF Files will have the same Name as the read fexported Files, with the Letters .gif attached.
uptonfiles=NFILES:
How many GIF Files to create. gd1.pp will try to read the first File, given by 1stinfile=FILENAME, and guess the next Files from the Name of the first File, ie. it will count up the trailing Number. It will read up to NFILES.
what= [absh | logabs]:
What to Display. The absolute Value of the Fieldstrength on the Material Patches, or the Logarithm of the absolute Value.
mpegfile:
The Name of the mpeg file to create from the many GIFs.
xrot= XROT, yrot= YROT, zrot= ZROT:
The Angles to rotate the Geometry around.
dxrot= DXROT, dyrot= DYROT, dzrot= DZROT:
The Increment of the Angles. The i.th plot will be rotated by XROT+(i-1)*DXROT around the x-Axis.
boxed:
Indicates whether a Box indicating the processed Volume shall be shown in the Plots.
doit:
The Files are read, the GIFs are generated, and it is tried to create a mpegfile from the GIFs.

GdfidL's command Language

Variables

A Variable has a Name and a Value. You define or redefine a Variable with the Sequence sdefine(name, value) or a Sequence define(name, value).

The Name of the Variable can be up to 32 Characters long. The Name must begin with an alphabetic Character and may contain Numbers and alphabetic Characters.
For sdefine(name, value), the Value of the Variable may be up to 132 Characters long. It may contain any Characters inside, except for '(\)'. Leading and trailing Blanks in the Value are ignored.
For define(name, expr), the Value of the Variable is the Value of the arithmetic Expression expr.

Whenever gd1 or gd1.pp encounter the Name of an already defined Variable, the Name is substituted by the Value of the Variable, and the Line is interpreted again.

Defining Variables from Outside

Both gd1 and gd1.pp can be supplied Options that define Variables from outside an Inputfile. The Syntax is gd1 -Dname=value. This way, you can e.g. compute Sispersion relations with simple Shell Scripts. Variables defined in this way are not automatically evaluated. ( sdefine(..,..) )
Example

#!/bin/sh
  # Given the proper "inputfile.gdf", this shell-Script computes the
  # dispersion Relation of some periodic Structure.
  for PHASE in 0 20 40 60 80 100 120 140 160 180
  do
      gd1 -DThisPhase=$PHASE < inputfile.gdf > out.Phase=$PHASE
  done

Arithmetic Expressions

Whenever gd1 or gd1.pp encounter the String eval(, the matching closing Brace is searched and the String inside the enclosing Braces is interpreted as an arithmetic Expression. The Value of the expression is transformed to a String and substituted for eval(expression).
Example

 echo (2*3)      # this outputs "(2*3)"
 echo eval(2*3)  # this outputs "6"

The arithmetic Expression may contain the arithmetic operators +,-,*,/,**,%. In addition to that, the boolean Operators ==,!=,<,>,<=,>= are handled. The result of applying a boolean Operator is an integer 0 or 1. Zero stands for false, and 1 for true.

The Functions abs(x), min(x,y), max(x,y), log(x), cos(x), sin(x), tan(x),
atan(x), atan2(x,y), mod(x,y), pow(x,y) are recognised and evaluated.

In every Context where a Number is required as a Parameter, an arithmetic Expression may be used. In these Contexts, enclosing the Expression in eval() is not required.

do-loops

Sections of the Input can be interpreted repeatedly via do loops: The Structure of a do loop is the same as in Fortran.

  do M1, M2, M3
     # Loop-Body
  enddo  # or 'end do'

The Loop-Body may itself contain do-loops, Macro Calls, whatever. The iteration Variable M1 is not restricted to Integer Values.

  do i= 1, 100, 1   # count upwards
     echo I is i
  end do
  do i= 100, 1, -1  # count downwards
     echo I is i
  end do
  do i= 1, 2, 0.1   # non integer step
     echo I is i
     echo 2*I is eval(2*i)
  end do

if elseif else endif

Conditional Interpretation of Part of an Inputfile is possible with if Blocks.
An if Block is:

  if (ARITHMETIC-EXPRESSION) then
     #
     # if-body
     #
  endif # or 'end if'

If the ARITHMETIC-EXPRESSION evaluates to something else than '0' then the Body of the If-Block is interpreted.

A general if block is:

  if (ARITHMETIC-EXPRESSION) then
     #
     # if-body
     #
  elseif (ARITHMETIC-EXPRESSION) then
     #
     # elseif-body
     #
  else
     #
     # else-body
     #
  endif

If-Blocks may be nested.

Macros

Anywhere in your Input you can define Macros. A Macro is enclosed between two Lines: The first Line contains the Keyword macro followed by the Name of the Macro. All Lines until a Line with only the Keyword endmacro are considered the Body of the Macro. When gd1 or gd1.pp find such a Macro, they read it and store the Body of the Macro in an internal Buffer.
Example

   #
   # This defines a macro with name 'foo'
   #
   macro foo
      echo I am foo, my first argument is @arg1
      echo The total number of arguments supplied is @nargs
   endmacro

When gd1 or gd1.pp find a Call of the Macro, the Number of the supplied Arguments is assigned to the Variable @nargs, and the Variables @arg1, @arg2, .. are assigned the Values of the supplied Parameters of the Call. Similiar to the user definable Variables (via sdefine), the Values of the Arguments are Strings. Of course, it is possible to have a String, e.g. '1e-4', which happens to be interpreted in the proper Context as a real Number.
Example

   #
   # this calls 'foo' with the arguments 'hi', 'there'
   #
   call foo(hi, there)

Macro Calls may be nested. The Body of a Macro may call another Macro.

Result-variables

gd1.pp makes its Results accessible as symbolic Variables. The Names of these Variables all start with @. The exact Name can be found in the Description of the Sections of gd1.pp. There are some other Variables as well that have not yet been described.

@pi, @clight: These are the Values of $\pi$ and of the Velocity of Light.

The following Variables are defined as soon as a Database has been specified:

@nx, @ny, @nz: These contain the Number of Grid Planes in the three coordinate Directions.
@x(i), @y(i), @z(i): These are the Positions of the i.th Gridplane.
@xmin, @xmax, @ymin, @ymax: These are the extreme Coordinates of the computational Volume.

gd1.pp has a special Variable @path. Its Value is a command String that would enter the current Section.

Supplied Macros

This Section documents four Macros that define a Sequence of secondary Computations to be performed in the Postprocessor gd1.pp. All four Macros are contained in the File
/usr/local/gd1/postprocessor-macros.

Q-Values

The quality Factor Q is defined as

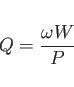$\begin{displaymath} Q = \frac{\omega W}{P} \end{displaymath}$

(4.1)

where

$\omega$ is the circular resonant Frequency,
is the total stored Energy,
is the total Power Loss due to Currents in lossy Materials.

In the Section -wlosses we compute the wall Wosses via the Perturbation Formula. In the Section -energy we compute the stored Energy in the H-Field.

Q-Values: Real valued Fields

The following macro contains the Commands to evaluate the above Formula for a given resonant Field. This Macro is contained in the file /usr/local/gd1/postprocessor-macros.

macro QValue
  pushflags, noprompt, nomenu, nomessage
  define(QValue_PATH, @path)                  # remember current section
  -base                                       # goto the base of the branch-tree
  -energy                                     # compute stored energy
      quantity= h                             # ... we dont need to compute the
      solution= @arg1                         #     energy in the electric field
      doit                                    #     -- it has to be the same
  -wlosses                                    # Wall-losses
      doit
 echo
echo *** h-Energy   is @henergy
echo *** metalpower is @metalpower
  return
  define(QValue_value, eval(2*@pi*@frequency*2*@henergy/@metalpower))
  echo *** mode number       is @arg1
  echo *** frequency         is @frequency {Hz}
  echo *** QValue            is QValue_value {1}
# echo return path is : QValue_PATH
  QValue_PATH                                 # back to where we came from ...
  undefine(QValue_PATH)
  popflags
endmacro

With the Definition of the Macro available, we can compute the Q-Value of the first resonant Mode by saying:

   call QValue(1)

To compute the Q-Values of the first five Modes, we may say:

 do i= 1, 5
    call QValue(i)
 enddo

Q-Values: Complex valued Fields

For complex Fields (resonant fields computed with periodic boundary conditions or lossy resonant Fields), we have to integrate over the Real and imaginary Part separately:

macro perQValue
  pushflags, noprompt, nomenu, nomessage
  define(perQValue_PATH, @path)               # remember current section
  -base                                       # goto the base of the branch-tree
  -energy                                     # compute stored energy
      quantity= hre                           # ... we dont need to compute the
      solution= @arg1                         #     energy in the electric field
      doit                                    #     -- it has to be the same
# echo *** W_h of real part is @henergy
      define(hre_energy, @henergy)
      quantity= him
      doit
      define(him_energy, @henergy)
define(htot_energy, eval(hre_energy+him_energy) )
  -wlosses                                    # Wall-losses
      quantity= hre, doit
      define(hre_metalpower, @metalpower)
      quantity= him, doit
      define(him_metalpower, @metalpower)
      define(htot_metalpower, eval(hre_metalpower+him_metalpower))
# echo *** total h-Energy   is htot_energy
# echo *** total metalpower is htot_metalpower
  define(perQValue_value, eval(2*@pi*@frequency*2*htot_energy/htot_metalpower))
  echo
  echo *** mode number       is @arg1
  echo *** frequency         is @frequency {Hz}
  echo *** QValue            is perQValue_value {1}
# echo return path is : perQValue_PATH
  perQValue_PATH                              # back to where we came from ...
  undefine(perQValue_PATH)
  popflags
endmacro

With the definition of the Macro available, we can compute the Q-Value of the first resonant Mode by saying:

   call perQValue(1)

To compute the Q-Values of the first five Modes, we may say:

 do i= 1, 5
    call perQValue(i)
 enddo

Computing normalised Shunt Impedances

There are several Definitions for a normalised Shunt Impedance floating around. We take this one:

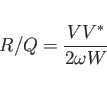$\begin{displaymath} R/Q = \frac{V V^*}{2 \omega W} \end{displaymath}$

(4.2)

where

is the normalised Shunt Impedance,
is the complex Voltage that would be seen by a Witness Charge traversing the Cavity at a Speed of $\beta c_0$ ,
$\omega$ is the circular Frequency of the Mode,
is the total stored Energy in the Cavity (both electric and magnetic Energy).

If one evaluates the Voltage seen by the Witness Particle, one arrives at the Result

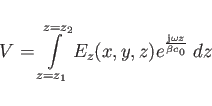$\begin{displaymath} V = \int\limits_{z=z_1}^{z=z_2} E_z(x,y,z) e^\frac{{\rm j}\omega z}{\beta c_0}\; dz \end{displaymath}$

(4.3)

for a Particle that travels in positive z-Direction from

R/Q: Real valued Fields

The following macro contains the Commands to evaluate the above Formula for a given Real-Valued resonant Field. This Macro is contained in /usr/local/gd1/postprocessor-macros.

macro rshunt
  pushflags, noprompt, nomenu, nomessage
  define(rshunt_PATH, @path)                # remember current section
  -base                                     # goto the base of the branch-tree
  -energy                                   # compute stored energy
      quantity= e                           # ... we dont need to compute the
      solution= @arg1                       #     energy in the magnetic field
      doit                                  #     -- it has to be the same
# echo *** W_e is @eenergy
  return
  -lintegral                                # accelerating voltage
      direction= z, component= z
      startpoint= (0,0, @zmin)
      length= auto
      doit
# echo *** vabs is @vabs
  return
  define(rshunt_value_a, eval(@vabs **2/(2*@pi*@frequency*(2*2*@eenergy))))
  define(rshunt_value_r, eval(@vreal**2/(2*@pi*@frequency*(2*2*@eenergy))))
  define(rshunt_value_i, eval(@vimag**2/(2*@pi*@frequency*(2*2*@eenergy))))
  echo
  echo *** mode number         is @arg1
  echo *** frequency           is @frequency {Hz}
  echo ***
  echo *** shunt impedances as computed from | U * conjg(U) | :
  echo *** Shunt Impedance/Q   is rshunt_value_a {Ohms}
  echo *** Shunt Impedance/Q/m is eval(rshunt_value_a/@length) {Ohms/m}
  echo ***
  echo *** shunt impedances as computed from | Re(U) * Re(U) | :
  echo *** Shunt Impedance/Q   is rshunt_value_r {Ohms}
  echo *** Shunt Impedance/Q/m is eval(rshunt_value_r/@length) {Ohms/m}
  echo ***
  echo *** shunt impedances as computed from | Im(U) * Im(U) | :
  echo *** Shunt Impedance/Q   is rshunt_value_i {Ohms}
  echo *** Shunt Impedance/Q/m is eval(rshunt_value_i/@length) {Ohms/m}

## echo return path is : rshunt_PATH
  rshunt_PATH                               # back to where we came from ...
  undefine(rshunt_PATH)
## echo return path is : rshunt_PATH
  popflags
endmacro

R/Q: Complex valued Fields

For complex valued Fields, we evaluate separately the real Part and the imaginary Part of the Field. This is done with the following macro:

macro perrshunt
  pushflags, noprompt, nomenu, nomessage
  define(rshunt_PATH, @path)                  # remember current section
  -base                                       # goto the base of the branch-tree
  -energy                                     # compute stored energy
      quantity= ere                           # ... we dont need to compute the
      solution= @arg1                         #     energy in the magnetic field
      doit                                    #     -- it has to be the same
# echo *** W_e of real part is @eenergy
      define(ere_energy, @eenergy)
      quantity= eim
      doit
      define(eim_energy, @eenergy)
define(etotenergy, eval(ere_energy+eim_energy) )
  return
  -lintegral                                  # accelerating voltage
      direction= z, component= z
      startpoint= (0,0, @zmin)
      length= auto
      quantity= ere, doit
# echo *** vabs of real part is @vabs
      define(V_ere_re, @vreal) define(V_ere_im, @vimag)
      quantity= eim, doit
# echo *** vabs of imaginary part is @vabs
      define(V_eim_re, @vreal) define(V_eim_im, @vimag)
  return
define(vztotre, eval(V_ere_re-V_eim_im))
define(vztotim, eval(V_ere_im+V_eim_re))
define(vztotabs, eval((vztotre**2+vztotim**2)**0.5) )
  define(rshunt_value, eval(vztotabs**2/(2*@pi*@frequency*(2*etotenergy))))
  echo
  echo *** mode number       is @arg1
  echo *** frequency         is @frequency {Hz}
  echo *** Shunt Impedance   is rshunt_value {Ohms}
  echo *** Shunt Impedance/m is eval(rshunt_value/@length) {Ohms/m}
# echo return path is : rshunt_PATH
  rshunt_PATH                                 # back to where we came from ...
  undefine(rshunt_PATH)
  popflags
endmacro

stp2stl: Converts STEP File to STL-File

A OpenCascade-based STEP to STL File Converter is provided. The Converter reads a STEP-File and writes a STL-File. The Parameter '-deflection=XX' controls the Accuracy of the generated STL-File. A sample Shell Script which generates two STL-Files from the same STEP-File but with different Values for '-deflection=XX' is shown below.

#!/bin/sh

 for DEFL in 1e-4 1e-5
 do
    $GDFIDL_HOME/Linux-x86_64/stp2stl \
        -infile=/usr/local/gd1/examples/Vac-Quart_12WNSDVG1.8.stp \
        -deflection=$DEFL -outfile=/tmp/UserName/$DEFL.stl
 done

Parts of the generated STL-Data are shown in Figures 5.1 and 5.2.

**Figure 5.1:** A Part of the STL-Data generated with deflection set to 1e-4
$\begin{figure}\epsfig{figure=stp2stl1.ps,width=18cm,bbllx=174pt,bblly=107pt,bburx=587pt,bbury=457pt,clip=} \end{figure}$

**Figure 5.2:** A Part of the STL-Data generated with deflection set to 1e-5
$\begin{figure}\epsfig{figure=stp2stl2.ps,width=18cm,bbllx=174pt,bblly=107pt,bburx=587pt,bbury=457pt,clip=} \end{figure}$

Examples

This Chapter shows some Examples for the Interplay of Device Description, Computation, and Postprocessing.

There is no Example for computing Eigenvalues, as this is mentioned in great Detail in the Tutorial.

Wake Potentials

The Computation of Wakepotentials occurs in two Steps.

gd1 is used to perform a Time-Domain Computation with an exciting relativistic Line-Charge.
Then, gd1.pp is used to compute the Wakepotentials from the Data that were recorded by gd1.

As a simple Example, we use a very strange Device where we want to compute the Wakepotentials of. The Input for gd1 is

 # /usr/local/gd1/examples-from-the-manual/wake-example-1.gdf

define(LargeNumber, 1000)
#
# The following picture shows a cut through the structure to be
# modelled and the variables associated to the lengths.
#
#
#                a               a               a
#        |<------------->|<-------------->|<----------->|
#
#                 -      ------------------
#                 ^      |                |
#               b |      |                |
#                 |      |                |
#        -----------------                ---------------  -
#        |                     beam                     |  |
#        |<-------------------------------------------->|  | d
#        |                                              |  |
#        ------------------------------------------------  -
#
#    x^
#    |-> z
#
 define( a, 1e-2 )
 define( b, 5e-3 )
 define( c, 5e-3 )
 define( d, 1e-2 )

 -general
    outfile= /tmp/UserName/wake-example
    scratch= /tmp/UserName/wake-example-scratch

    text()= A strange Device,
    text()= it serves only as an Example
    text()= for computing Wakepotentials.

 -mesh
define(STPSZE, 3*a/60 )
    spacing= STPSZE
    perfectmesh= no

    pxlow= 0, pxhigh= c+b
    pylow= -STPSZE, pyhigh= d
    pzlow= 0, pzhigh= 3*a

    cxlow= ele, cxhigh= ele
    cylow= ele, cyhigh= ele
    czlow= ele, czhigh= ele

    #
    # We enforce a Meshline at the Position of the Linecharge
    # by enforcing two Meshplanes.
    #
    xfixed(1, c/2, 0)
    yfixed(1, d/2, 0)

 -brick
    #
    # Fill the universe with Metal.
    #
    material= 1
       volume= (-LargeNumber, LargeNumber,\
                -LargeNumber, LargeNumber,\
                -LargeNumber, LargeNumber)
    doit

    #
    # Carve out the Waveguide.
    #
    mat 0
       xlow= 0, xhigh= c
       ylow= 0, yhigh= LargeNumber
       zlow= -LargeNumber, zhigh= LargeNumber
    doit

    #
    # Carve out the Resonator Box.
    #
    mat 0
       xlow= 0, xhigh= c+b
       ylow= 0, yhigh= LargeNumber
       zlow= a, zhigh= 2*a
    doit

 -volumeplot
   eyepos= ( 1.0, 2.30, 0.5 )
   showlines= yes
   scale= 2.5
   doit

 -fdtd
    -ports
       name= zlow, plane= zlow, modes= 0, doit
       name= zhigh, plane= zhigh, modes= 0, doit

    -lcharge
       charge= 1e-12   # 1 pAs
       sigma= 5e-3
       xposition= c/2
       yposition= d/2

 -fdtd
     doit

**Figure 6.1:** This Volumeplot shows the discretised Device. Although **gd1** allows an inhomogeneous Mesh even when a particle Beam is present, this is not explicitely used here.
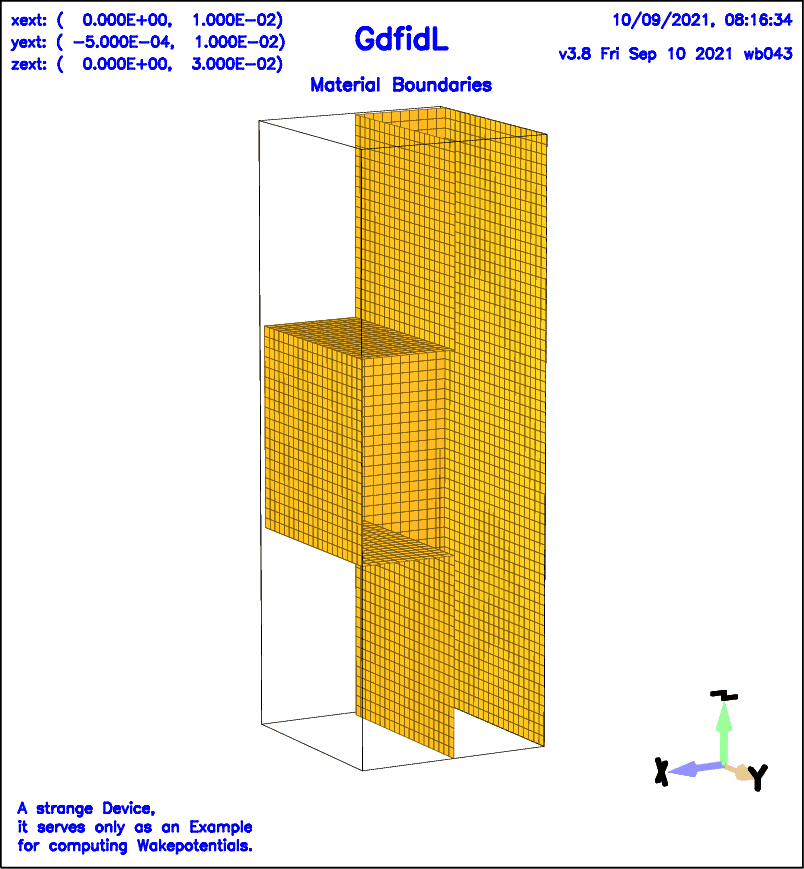$\begin{figure}\centerline{ \psfig{figure=wake-example00.ps,width=18cm,bbllx=25pt,bblly=197pt,bburx=586pt,bbury=802pt,clip=} }\end{figure}$

We start gd1 with the UNIX-Command:

   gd1 <  wake-example-1.gdf | tee out

The next Step is to tell the Postprocessor that we wish to see the Wakepotentials: The Commands for the Postprocessor gd1.pp are:

 -general, infile= @last
 -wakes
    doit

We get three Plots for the three Components of the Wakepotential at the (x,y) Position where the Line-Charge was travelling.

**Figure 6.2:** The z-Component of the Wakepotential at the (x,y)-Position where the exciting Line-Charge was travelling. For Reference, the Shape of the exciting Charge is plotted as well.
$\begin{figure}\centerline{ \psfig{figure=wake-example00.wz.ps,width=14cm,bbllx=0pt,bblly=43pt,bburx=776pt,bbury=575pt,clip=} }\end{figure}$

$\begin{figure}\centerline{ \psfig{figure=wake-example00.wx.ps,width=14cm,bbllx=0pt,bblly=43pt,bburx=776pt,bbury=575pt,clip=} } \end{figure}$

**Figure 6.3:** The two transverse Components of the Wakepotential at the (x,y)-Position where the exciting Line-Charge was travelling. For Reference, the Shape of the exciting Charge is plotted as well. The transverse Wakepotentials are computed as the Average of the transverse Wakepotentials nearest to the Position where the Line-Charge was travelling. The y-Component of the Wakepotential vanishes, as it should be.
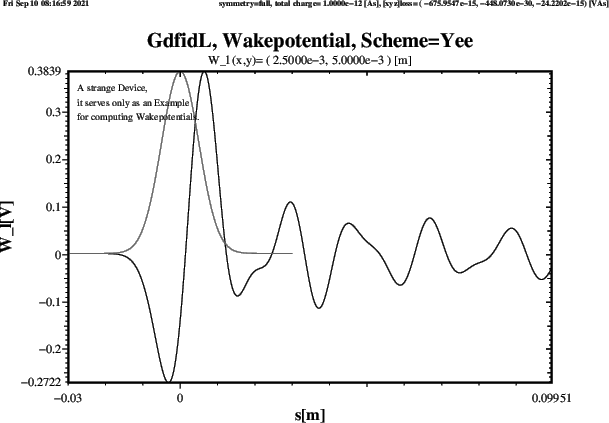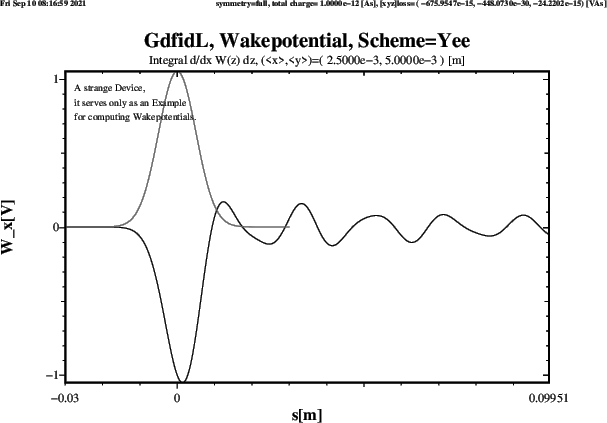
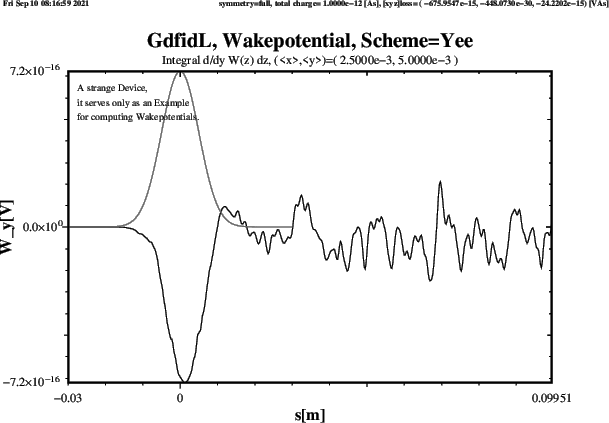$\begin{figure}\centerline{ \psfig{figure=wake-example00.wy.ps,width=14cm,bbllx=0pt,bblly=43pt,bburx=776pt,bbury=575pt,clip=} }\end{figure}$

Scattering Parameters

The Computation of scattering Parameters is via two Steps.

gd1 is used to perform a Time-Domain Computation with an excited Port Mode.
Then gd1.pp is used to compute the scattering Parameters from Data that were recorded by gd1.

As a simple Example, we use a somewhat strange Device where we want to compute the scattering Parameters of. The Input for gd1 is

 # /usr/local/gd1/examples-from-the-manual/spar-example-1.gdf

 define(LargeNumber, 1000)

 define( a, 1e-2 )
 define( b, 5e-3 )
 define( c, 5e-3 )
 define( d, 1e-2 )

 define(FREQ, 20e9)

 -general
    outfile= /tmp/UserName/spar-example
    scratch= /tmp/UserName/spar-example-scratch

    text()= A strange Geometry, just an Example.

 -mesh
 define(STPSZE, 3*a/60 ) # Too large for MPI
# define(STPSZE, a/60 )
    spacing= STPSZE
    graded= yes, qfgraded= 1.2, dmaxgraded= @clight / FREQ / 40
    perfectmesh= no

    pxlow= 0, pxhigh= c+b
    pylow= -STPSZE, pyhigh= d
    pzlow= 0, pzhigh= 3*a

    cxlow= ele, cxhigh= ele
    cylow= ele, cyhigh= ele
    czlow= ele, czhigh= ele

 -brick
    #
    # Fill the Universe with Metal.
    #
    material= 1
       volume= (-LargeNumber, LargeNumber,\
                -LargeNumber, LargeNumber,\
                -LargeNumber, LargeNumber)
    doit

    #
    # Carve out the Waveguide.
    #
    mat 0
       xlow= 0, xhigh= c
       ylow= 0, yhigh= LargeNumber
       zlow= -LargeNumber, zhigh= LargeNumber
    doit

    #
    # Carve out Resonator Box.
    #
    mat 0
       xlow= 0, xhigh= c+b
       ylow= 0, yhigh= LargeNumber
       zlow= a, zhigh= 2*a
    doit

 -volumeplot
   eyepos= ( 1.0, 2.30, 0.5 )
   showlines= yes
   scale= 3
   doit

 -fdtd
    -ports
       name= Input, plane= zlow, modes= 1, doit
       name= Output, plane= zhigh, modes= 1, doit

    -pexcitation
       port= Input
       mode= 1
       amplitude= 1
       frequency= FREQ
       bandwidth= 0.7*FREQ

    -time
       #
       # tminimum: the minimum Time to be simulated
       # tmaximum: the maximum Time to be simulated
       #   If the Amplitudes have died down sufficiently
       #   at a Time between tmin and tmax,
       #   the Computation will stop.
       #
       tmin=   10/FREQ
       tmax= 1000/FREQ
       amptresh= 1e-3

 -fdtd
     doit

**Figure 6.4:** This Volumeplot shows the discretised Geometry.
$\begin{figure}\centerline{ \psfig{figure=spar-example00.ps,width=18cm,bbllx=25pt,bblly=197pt,bburx=586pt,bbury=803pt,clip=} }\end{figure}$

We start gd1 with the Unix-Command:

   gd1 < spar-example-1.gdf | tee out

The next Step is to tell the Postprocessor that we wish the scattering Parameters to be computed and plotted. In addition to the default Values, we want to see (Parts of) the Timedata that were recorded during the Time-Domain Computation, and we want to see the scattering Parameters in a Smith-Chart. The Commands for the Postprocessor gd1.pp are:

 -general, infile= @last
 -sparameter
    ports= all, modes= 1
    timedata= yes
    smithplot= yes, markerat 19e9, markerat 20e9, markerat 21e9
    doit

We get in total 9 Plots.

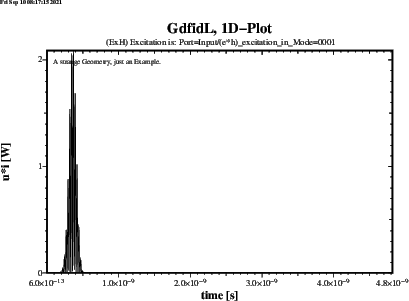
$\begin{figure}\centerline{ \psfig{figure=spar-example00-excitation.0001.ps,width=10cm,bbllx=0pt,bblly=43pt,bburx=776pt,bbury=575pt,clip=} } \end{figure}$

**Figure 6.5:** The Data of the Excitation. Above: The time History of the Amplitude that was excited in the Port with Name 'Input'. Below: The Spectrum of this Excitation.
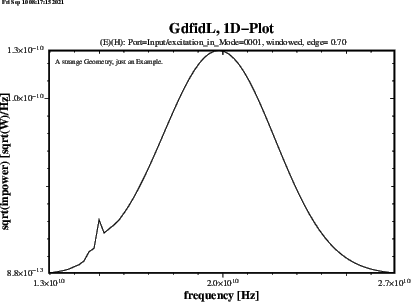$\begin{figure}\centerline{ \psfig{figure=spar-example00-excitation.0002.ps,width=10cm,bbllx=0pt,bblly=43pt,bburx=776pt,bbury=575pt,clip=} }\end{figure}$

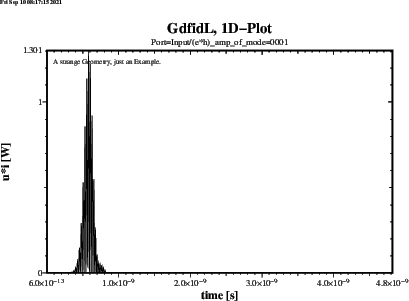
$\begin{figure}\centerline{ \psfig{figure=spar-example00-Input-e_amp_of_mode-eq-0... ...ps,width=10cm,bbllx=0pt,bblly=43pt,bburx=776pt,bbury=575pt,clip=} } \end{figure}$

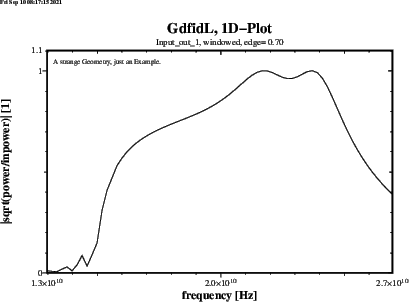
$\begin{figure}\centerline{ \psfig{figure=spar-example00-Input_out_1-freq-abs.ps,width=10cm,bbllx=0pt,bblly=43pt,bburx=776pt,bbury=575pt,clip=} } \end{figure}$

**Figure 6.6:** The Data of the scattered Mode '1' in the Port with Name 'Input'. Above: The time History of its Amplitude. This was computed by **gd1**. Below: The scattering Parameter as Amplitude Plot, and in a Smith-Chart. These Data are computed by **gd1.pp** by Fourier-Transforming the time History of this Mode, and dividing by the Spectrum of the Excitation.
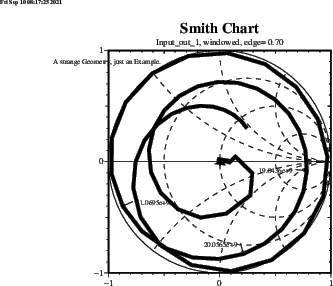$\begin{figure}\centerline{ \psfig{figure=spar-example00-Input_out_1-freq-smith.ps,width=10cm,bbllx=0pt,bblly=43pt,bburx=776pt,bbury=575pt,clip=} }\end{figure}$

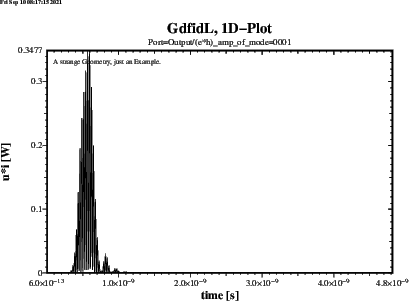
$\begin{figure}\centerline{ \psfig{figure=spar-example00-Output-e_amp_of_mode-eq-... ...ps,width=10cm,bbllx=0pt,bblly=43pt,bburx=776pt,bbury=575pt,clip=} } \end{figure}$

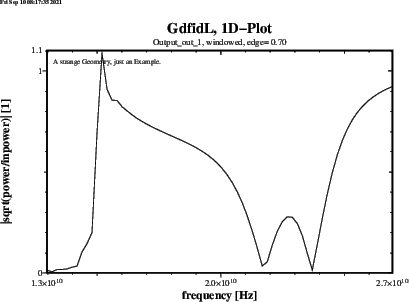
$\begin{figure}\centerline{ \psfig{figure=spar-example00-Output_out_1-freq-abs.ps,width=10cm,bbllx=0pt,bblly=43pt,bburx=776pt,bbury=575pt,clip=} } \end{figure}$

**Figure 6.7:** The Data of the scattered Mode '1' in the Port with Name 'Output'. Above: The time History of its Amplitude. This was computed by **gd1**. Below: The scattering Parameter as Amplitude Plot, and in a Smith-Chart. These Data are computed by **gd1.pp** by Fourier-Transforming the time History of this Mode, and dividing by the Spectrum of the Excitation.
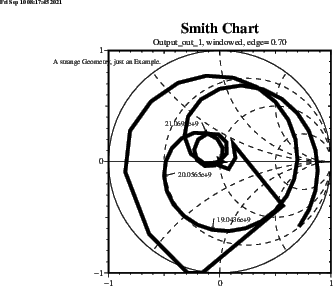$\begin{figure}\centerline{ \psfig{figure=spar-example00-Output_out_1-freq-smith.ps,width=10cm,bbllx=0pt,bblly=43pt,bburx=776pt,bbury=575pt,clip=} }\end{figure}$

**Figure 6.8:** The Sum of the squared scattering Parameters. Since the Device is loss-free, this Sum should ideally be identical to '1' above the cut-off Frequency. The Sum of the computed Parameters is only very near the cut-off Frequency of the Modes unequal '1'.
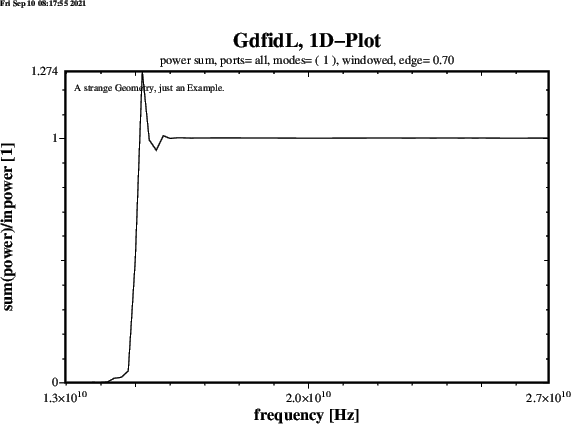$\begin{figure}\centerline{ \psfig{figure=spar-example00-sum-power-freq.ps,width=14cm,bbllx=0pt,bblly=43pt,bburx=776pt,bbury=575pt,clip=} }\end{figure}$

Computing Brillouin-Diagrams

Brillouin Diagrams are Plots of Eigenvalues (resonante Frequencies) as a Function of the Phase-Shift in periodic Structures. GdfidL allows Computation with specified Phase Shifts in x- y- and z-Direction simultaneously. So we can compute Brillouin diagrams in 3D-Periodic Structures, where the Plane-Normals of the Planes of Periodicity are in x- y- and z-Direction simultaneously.

The following Input defines an elemental Cell of such a periodic Structure.

 # /usr/local/gd1/examples-from-the-manual/brillo.gdf

 #
 # Assign a value to "PHASE", if it is not yet defined
 # via  "gd1 -DPHASE=XX"
 #
 if (! defined(PHASE) ) then
    define(PHASE, 45)
 endif

 #
 # What Part of the Brillouin-diagram do we want to compute?
 #
 #
 # part==1 : from Gamma to H : 0<kx<pi/d, ky=0,      kz=0
 # part==2 : from H to N     : kx=pi/d,   0<ky<pi/d, kz=0
 # part==3 : from N to P     : kx=pi/d,   ky=pi/d,   0<kz<pi/d
 # part==4 : from P to Gamma : 0 < (kx=ky=kz) < pi/d
 #

 #
 # Get the Value of PART by inclusion of a File:
 # the Content of the File is just
 #    "define(PART, 1)"
 # or "define(PART, 2)"
 # or "define(PART, 3)"
 # or "define(PART, 4)"
 include(this-part-of-brillo)

 if ( PART == 1 ) then
    define(XPHASE, PHASE)
    define(YPHASE, 000)
    define(ZPHASE, 000)
 endif

 if ( PART == 2 ) then
    define(XPHASE, 180)
    define(YPHASE, PHASE)
    define(ZPHASE, 000)
 endif

 if ( PART == 3 ) then
    define(XPHASE, 180)
    define(YPHASE, 180)
    define(ZPHASE, PHASE)
 endif

 if ( PART == 4 ) then
    define(XPHASE, PHASE)
    define(YPHASE, PHASE)
    define(ZPHASE, PHASE)
 endif

 define(INF, 10000.0 * @clight)
 define(MAG, 2) define(EL, 1)

 ##
 ## Geometry definitions
 ##
 define(LATTICE_D, @clight / 2 )
 define(RADIUS, LATTICE_D * 0.375 )

 #
 # Default Mesh Spacing.
 #
 define(STPSZE, RADIUS/10 )

 ##############
 ##############
 ##############
 ##############
 ##############
 -general
    outfile= /tmp/UserName/outfile
    scratchbase= /tmp/UserName/delete-me-

    text()= Lattice Constant d= LATTICE_D
    text()= Radius of the Spheres= RADIUS
    text()= r/d = eval(RADIUS/LATTICE_D)
    text()= 2r/d = eval(2*RADIUS/LATTICE_D)
    text()= stpsze= STPSZE
    text()= xphase: XPHASE
    text()= yphase: YPHASE
    text()= zphase: ZPHASE

 -mesh
    spacing= STPSZE
    graded= yes, dmaxgraded= 10*STPSZE
    qfgraded= 1.3
    perfectmesh= yes
 perfectmesh= no

    pxlow= -0.5*LATTICE_D, pxhigh= 0.5*LATTICE_D
    pylow= -0.5*LATTICE_D, pyhigh= 0.5*LATTICE_D
    pzlow= -0.5*LATTICE_D, pzhigh= 0.5*LATTICE_D

    xperiodic= yes, xphase= XPHASE
    yperiodic= yes, yphase= YPHASE
    zperiodic= yes, zphase= ZPHASE

    do ii= -1, 1, 1
       xfixed( 2, ii*LATTICE_D-RADIUS, ii*LATTICE_D+RADIUS )
       xfixed( 2, (ii-0.1)*LATTICE_D, (ii+0.1)*LATTICE_D )

       yfixed( 2, ii*LATTICE_D-RADIUS, ii*LATTICE_D+RADIUS )
       yfixed( 2, (ii-0.1)*LATTICE_D, (ii+0.1)*LATTICE_D )

       zfixed( 2, ii*LATTICE_D-RADIUS, ii*LATTICE_D+RADIUS )
       zfixed( 2, (ii-0.1)*LATTICE_D, (ii+0.1)*LATTICE_D )
    enddo

 ##############

 -brick
    #
    # Fill the Universe with Vacuum.
    #
    material= 0
       volume= (-INF,INF, -INF,INF, -INF,INF)
    doit


 define(M3, 1)
 #
 # Define square Lattice.
 # Only a Part of these Spheres end up being within
 # computational Volume.
 #
 do iz= 0, 1, 1
    do ix= 0, 1, 1
       do iy= 0, 1, 1
          #
          # A Sphere with Center at
          # ( ix*LATTICE_D, iy*LATTICE_D, iz*LATTICE_D )
          #
          -gbor
             material= M3
                origin= ( ix*LATTICE_D, \
                          iy*LATTICE_D, \
                          iz*LATTICE_D )
                rprimedirection= ( 1, 0, 0 )
                zprimedirection= ( 0, 0, 1 )
                range= ( 0, 360 )

                clear
                point= ( -RADIUS, 0 )
                   arc, radius= RADIUS, type= clockwise, size= small
                point= ( RADIUS, 0)
             doit
       enddo
    enddo
 enddo

 #
 # The connecting Rods in x-Direction.
 #
 do iz= 0, 1, 1
    do iy= 0, 1, 1
       -gccylinder
          material= M3
             radius= 0.1*LATTICE_D
             length= INF
             origin= ( -INF/2, \
                       iy*LATTICE_D, \
                       iz*LATTICE_D )
             direction= ( 1, 0, 0 )
          doit
    enddo
 enddo

 #
 # The Connecting Dods in y-Direction.
 #
 do iz= 0, 1, 1
    do ix= 0, 1, 1
       -gccylinder
          material= M3
             radius= 0.1*LATTICE_D
             length= INF
             origin= ( ix*LATTICE_D, \
                       -INF/2, \
                       iz*LATTICE_D )
             direction= ( 0, 1, 0 )
          doit
    enddo
 enddo

 #
 # The connecting Rods in z-Direction.
 #
 do ix= 0, 1, 1
    do iy= 0, 1, 1
       -gccylinder
          material= M3
             radius= 0.1*LATTICE_D
             length= INF
             origin= ( ix*LATTICE_D, \
                       iy*LATTICE_D, \
                       -INF/2 )
             direction= ( 0, 0, 1 )
          doit
    enddo
 enddo

 #
 # Definition of the Material Properties.
 #
 -material
    material= M3, type= electric


 #
 # What does the Materialdistribution look like?
 #
 -volumeplot
##    doit

 #################
 #
 # Computation of the Eigenvalues.
 #
 -eigenvalues
    solutions= 20
    estimation= 2.8
    pfac2= 1e-2
    passes= 2

    doit

 end

To compute the four Parts of the Brillouin-Diagram, we use a Shell-Script. This Shell-Script starts a Program four times. That Program starts gd1 several times to compute the Frequencies for different Phase-Shifts. This is the Shell-Script:

#!/bin/sh

 #
 # Compile the program which starts "gd1" several times
 #
 f77 brillo.f -o brillo.a.out

 for part in 1 2 3 4
 do
    #
    # (re)create the file that defines which part of the
    # Brillouin diagram is to be computed:
    #
    echo "define(PART, $part)" > this-part-of-brillo

    #
    # compute..
    ./brillo.a.out

    #
    # save the result, and display
    #
    cp brillo.mtv brillo.part=$part.mtv
    mymtv brillo.part=$part.mtv &

 done

 #
 # compile the program that combines the four parts
 # to a single Brillouin diagram of a 3D structure,
 # execute it,
 # and display the result..
 #
 f90 a3dbrillo.f
 cat brillo.part=[1-4].mtv | a.out
 mymtv2 3D-brillo.mtv &

The following is the Source of the Program that starts gd1 several times to compute the Frequencies for different Phase-Shifts:

!
! /usr/local/gd1/examples-from-the-manual/brillo.f90
!
 PROGRAM Bla

 IMPLICIT NONE
 CHARACTER(LEN= 400) cmd

 REAL, DIMENSION(300,1000) :: f0
 REAL, DIMENSION(1000) :: ph0

 INTEGER :: i11, i19, NMode, np, ip, Mode, iDum
 REAL :: af, ap, p0, p1, Phase, Acc, f

    i11= 11
    i19= 19
    OPEN (UNIT= i19, &
          FILE= 'brillo.mtv')

    WRITE (UNIT= i19, FMT= 90)
 90 FORMAT( &
      '$ DATA= CURVE2D NAME= "Brillouin-Diagramm"',/, &
      '% linetype= 0',/, &
      '% markertype= 3',/, &
      '% equalscale= false',/, &
      '% fitpage= false',/, &
      '% xyratio= 3',/, &
      '% xlabel= "Phase-shift"',/, &
      '% ylabel= "Frequency"',/, &
      '% comment= "no comment"',/  )

    af= 0
    ap= 0

    NMode= 15

! p0: First Phase
! p1: Last Phase
! np: Number of Phases

    p0= 0.
    p1= 180.
    np= 41

    DO ip= 1, np, 1
       Phase= p0+(ip-1)*(p1-p0)/FLOAT(np-1)
       ph0(ip)= Phase
       WRITE (UNIT= cmd, FMT= 81) Phase
 81    FORMAT( &
         ' gd1 "-DPHASE=', F8.2, '"< brillo.gdf ', &
         '| tee brillo.tmp | grep "for me" > brillo.out' )
 write (UNIT= 0, FMT= '(1X,4711(A))') ' cmd:', TRIM(cmd)
       CALL system( cmd )
       OPEN (UNIT= i11, &
             FILE= 'brillo.out')
       Mode= 0
  100    CONTINUE
       DO
          READ (UNIT= i11, FMT= *, ERR= 199, END= 199) iDum, f, acc
          IF (acc < 0.5) THEN
             Mode= Mode+1
             IF (Mode <= NMode) f0(Mode,ip)= f
             WRITE (UNIT= i19, FMT= 71) Phase,f
 write (0,*) Phase, f, acc
             af= MAX(af, f)
             ap= MAX(ap, Phase)
          END IF
       END DO
 199   CONTINUE
       CLOSE (UNIT= i11)
    END DO

 71 FORMAT( '@ point x1=', 1P, E12.6, ' y1=', E12.6, &
            ' z1= 0 markertype=1', ' markersize= 1' )

    DO Mode= 1, NMode, 1
       WRITE (UNIT= i19, FMT= *)
       DO ip= 1, np, 1
          WRITE (UNIT= i19, FMT= *) ph0(ip),f0(Mode,ip)
       END DO
    END DO
    WRITE (UNIT= i19, FMT= *)
    WRITE (UNIT= i19, FMT= 99) 0., 0., 0., af, ap, af
 99 FORMAT( 3(1X, 1P, 2(E12.6, 1X), /), /)
!
!   **
!   ** write the uninterpreted data
!   **
!
    DO ip= 1, np, 1
       WRITE (UNIT= i19, FMT= '(//,A,F14.2)') ' # Phase:', ph0(ip)
       DO Mode= 1, NMode, 1
          WRITE (UNIT= i19, FMT= '(A,1X,1P,E20.7)') '#', f0(Mode,ip)
       END DO
    END DO

 END PROGRAM Bla

The resulting Plots are presented in figure 6.9.

**Figure 6.9:** The four Parts of the Brillouin-Diagram.
$\begin{figure}\centerline{ \psfig{figure=brillo.part1-4.PS,width=10.5cm} }\end{figure}$

The following is the Sourcecode of the Program that combines the four Parts of the Brillouin-Diagram into a single Plot:

*
* /usr/local/gd1/examples-from-the-manual/a3dbrillo.f
*
* usage:
*
* cat brillo.part=[1-4].mtv | a.out
* mymtv2 3D-brillo.mtv
*
*
      DIMENSION f0(300,1 000), ph0(1 000)
      REAL, DIMENSION(100) :: Phase0, scale
      CHARACTER(LEN=1000) :: str
*
      i11= 11
      i19= 19
      OPEN (UNIT= i19
     1    , FILE= '3D-brillo.mtv')
*
      WRITE (UNIT= i19, FMT= 9000)
 9000 FORMAT(
     1 '$ DATA= CURVE2D NAME= "Brillouin-Diagramm"',/,
     2 '% linetype= 0',/,
     3 '% markertype= 3',/
     4 '% equalscale= false',/,
     5 '% fitpage= false',/,
     6 '% xyratio= 3',/,
     7 '% xlabel= "normalised Phase-shift"',/,
     8 '% ylabel= "Frequency"',/,
     9 '% comment= "no comment"',/
     x )
*
      af= 0.
      ap= 0.
*
      NMode= 10
*
      phase0(1:4)= (/ 0.0,
     1                1.0,
     2                2.0,
     3                4.0  /)
      scale(1:4)= (/ 1./180.0,    !! Gamma to H
     2               1./180.0,    !!     H to N
     3               1./180.0,    !!     N to P
     4              -1./180.0 /)  !!     P to Gamma
*
      Phase Last= 0.
      np= 1
      str= ' '
      DO
         DO
            IF (INDEX(str, '# phase:') .NE. 0) THEN
               jj= INDEX(str, '# phase:')+LEN('# phase:')
               READ (UNIT= str(jj:), FMT= *) phase
               IF (phase .LT. Phase Last) THEN
                  np= np+1
               ENDIF
               Phase Last= phase
               EXIT
            ENDIF
            READ (UNIT= *, FMT= '(A)', END= 10) str
         ENDDO
      write (*,*) ' phase:', phase
         pp= Phase0(np)
         ph0(np)= pp+phase*scale(np)
*
         mode= 0
         DO mode= 1, NMode, 1
            READ (UNIT= *, FMT= '(A)', END= 10) str
            READ (UNIT= str(2:), FMT= *, IOSTAT= iostat) f
            IF (iostat .NE. 0) EXIT
      write (*,*) ' pp, f:', pp+phase*scale(np), f
            f0(mode,np)= f
            WRITE  (UNIT= i19, FMT= 7010) pp+phase*scale(np),f
            af= MAX(af,f)
            ap= MAX(ap,pp+phase*scale(np))
         ENDDO
      ENDDO
   10 CONTINUE
*
 7010 FORMAT(
     1 '@ point x1=',E12.6,' y1=',E12.6,' z1= 0 markertype=1',
     2 ' markersize= 1')
*
      WRITE (UNIT= i19, FMT= *)
      WRITE (UNIT= i19, FMT= 99) 0.,0.,0.,af,ap,af
 99 FORMAT(3(' ',2(E12.6,' ')/),/)
*
      END

The resulting Plot is presented in Figure 6.10.

**Figure 6.10:** The four Parts of the Brillouin-Diagram combined.
$\begin{figure}\centerline{ \psfig{figure=a3dbrillo.PS,width=10.5cm} }\end{figure}$

This is the End of this Document

Footnotes

... File ^1.1: This will actually be a Directory. The Reason is: For current (2014) Workstations, it is quite easy to generate Data in excess of 2GBytes. But many current Filesystems and OS-Tools cannot handle Files larger than 2GBytes. So we chose to organise the computed Data as a Hierarchy of Files. A Directory is a Hierarchy of Files, so we used just that.
... stop.^1.2: This was implemented for some User who uses this Facility to use a Queue for short running Jobs for his long running Jobs. He puts a Computation which will run for eg 10 Hours into a Queue where Jobs are killed after running for more than 1 Hour. He instructs GdfidL to write these Restartfiles and stop after writing them. After a Job was run for less than 1 Hour, a Script inspects the Logfiles, and if the Computation needs to continue, the next Job is put into the short-Runner Queue, which uses the previously written Restartfiles to continue the Job.
... System ^1.3: AutoCAD can export its Data as a STL-file. The Command is 'stlout'.
... T\"uckmantel ^1.4: J. Tückmantel, `Urmel with a High Speed and High Precision Eigenvector Finder', CERN/EF/RF 83-5, 11 July 1983
...4 ^1.5: J. Tückmantel `An improved version of the eigenvector processor SAP applied in URMEL', CERN/EF/RF 85-4, 4 July 1985